チェバ・メネラウスの定理の逆

チェバの定理・メネラウスの定理の逆について見ていきます。

・チェバ・メネラウスの定理の逆の注意点
チェバの定理もメネラウスの定理も結論の分数式が同じなので、そのままの内容で逆を考えることができません。そこで辺またはその延長上にある\(P,Q,R\)の個数に着目して場合分けすることになります。

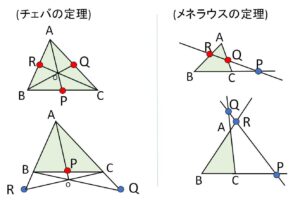
図より\(P,Q,R\)について
チェバの定理
・辺上に3個(延長上に0個)
・辺上に1個(延長上に2個)
メネラウスの定理
・辺上に2個(延長上に1個)
・辺上に0個(延長上に3個)

なので、これらの交点の個数の前提が必要です。さらにチェバの定理では延長上に交点が2個あるケースでは、\(AP,BQ,CR\)が平行になり交点\(O\)が無い場合があるのでこれも除外する必要があります。

・チェバの定理の逆

(解説)

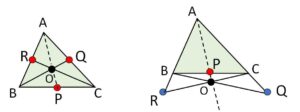
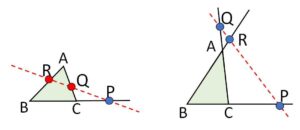
先ほどの説明の通り、辺上にある個数が1個,3個という条件が必要です。また\(BQ,CR\)が平行になってしまう場合もあるので除外します。例えば下図では
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}\)
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{1}\cdot\displaystyle\frac{2}{1}=1\)
が成り立っていますが、3直線は1点で交わっていません。

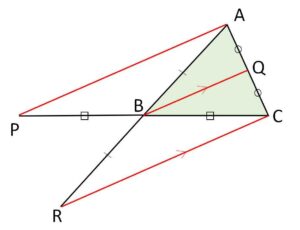
ところでチェバの定理の逆の内容はやや複雑ですが、細かい部分を除けば
「\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)　・・・(i) \(→\) 3直線は1点で交わる」
ということで、結論は3直線が1点で交わることです。よって三角形の五心において1点で交わるという証明などにも利用できます。

なお元のチェバの定理では交点\(O\)が三角形を作る直線上にない、つまり\(P,Q,R\)が頂点にないという条件がありましたが、チェバの定理の逆では\(P,Q,R\)が頂点にあると(i)の分数の分子または分母が\(0\)になってしまう箇所があり、そもそも仮定である(i)式が成り立たないので特に文言は不要です。((i)式にその内容は含まれるということ)

証明は同一法(一致法)を利用します。(メネラウスの定理の逆の証明も同じ)

(証明)

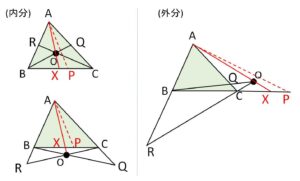
(比だけだと内分・外分のパターンがあるので場合分けします)

\(P\)が辺\(BC\)上にあるとき(\(R,Q\)がともに辺上ある or ともに延長上にある)、\(BQ,CR\)の交点を\(O\)とすれば、\(O\)は\(\angle A\)の内角(またはその対頂角)の内側にあるので、\(AO\)を結ぶと\(BC\)と辺上で交わる(左図)。この交点を\(X\)とするとチェバの定理より
\(\displaystyle\frac{BX}{XC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
また仮定より
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
よって
\(\displaystyle\frac{BX}{XC}=\displaystyle\frac{BP}{PC}\)
\(X,P\)はともに辺上にあるから、\(X,P\)は一致し3直線は1点\(O\)で交わる。

\(P\)が辺\(BC\)の延長上にあるとき(\(R,Q\)が辺上、延長上に1つずつ)、\(BQ,CR\)の交点を\(O\)とすれば、\(O\)は\(\angle A\)の外角の内側にあるので、\(AO\)を結ぶと\(BC\)と辺の延長上で交わる(右図)。よってその交点を\(X\)とすれば\(X,P\)がともに延長上にあることから、あとはチェバの定理を利用すれば同様に示せる。

・メネラウスの定理の逆

(解説)

最初の説明により延長上にある\(P,Q,R\)の個数が、1個または3個という前提が必要です。辺上にある個数が0個または2個としてもよいです。
メネラウスの定理の逆の結論は3点が一直線上にあるということなので、3点が同一直線上にある証明などに利用できます。証明方法はチェバの定理の逆と同じです。

(証明)

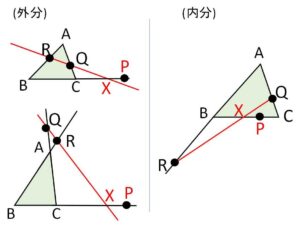
\(P\)が\(BC\)の延長上にあるとき(\(Q,R\)がともに辺上 または ともに延長上)、\(QR\)を結ぶと\(BC\)と辺\(BC\)の延長上で交わる(左図)。この交点を\(X\)とするとメネラウスの定理より
\(\displaystyle\frac{BX}{XC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
また仮定より
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
よって
\(\displaystyle\frac{BX}{XC}=\displaystyle\frac{BP}{PC}\)
\(X,P\)はともに延長上にあるから、\(X,P\)は一致し3点\(P,Q,R\)は一直線上にある。

\(P\)が辺\(BC\)上にあるとき(\(Q,R\)が辺上、延長上に1つずつ)、\(QR\)を結ぶと\(BC\)と辺\(BC\)上で交わる(右図)。この交点を\(X\)とすると\(X,P\)はいずれも辺\(BC\)上にあるので、あとはメネラウスの定理を用いれば証明できる。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→チェバ・メネラウスの定理の逆(演習)　back→メネラウスの定理