内接四角形の定理

円に内接する四角形の特徴について見ていきます。

 

・内接四角形の定理
円周角の定理を利用すると、内接四角形の対角の和について次のことが言えます。

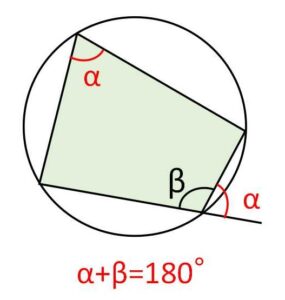
(解説)
円周上に多角形の頂点のすべてがあるとき、この多角形は円に内接するといいその円は外接円とよびます(外側に円があるので外接円)。上記定理の証明は円周角の定理(中心角に着目する)を利用すると証明可能です。なお(1)(2)の表す内容はほとんど同じです。

(証明)

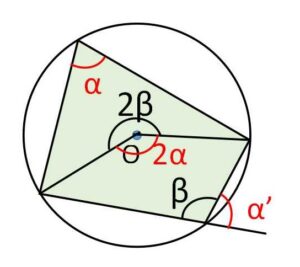
図の\(α,β\)に対する中心角は\(2α,2β\)であり
\(2α+2β=360°\)
だから
\(α+β=180°\)・・・(1)
よって対角の和は\(180°\)。

また\(β\)の外角を\(α’\)とすると
\(α’+β=180°\)
これと(1)より
\(α=α’\)・・・(2)
よって内角は対角の外角と等しい。

 

 

・四角形が円に内接するための条件
先ほどの定理とは逆に四角形が円に内接する条件を考えてみます。一般に三角形の3頂点を通る円(外接円)は常に存在しますが、4点を通る円は存在するとは限らないので四角形はある条件が整わないと円に内接しません。その条件は先ほどの定理の結果と同じです。

(解説)
(1)(2)の表す内容はほとんど同じです。円に内接することが分かれば(共通の円を発見できれば)、円周角の定理や半径が一定であることなどから角度や長さを求めたり証明問題にも利用できます。

(証明)

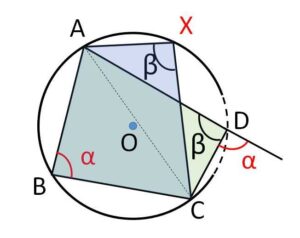
(\(△ABC\)の外接円\(O\)を考えます。\(D\)はこの円周上にあるかどうかは不明(それを証明したい)なので、円周上に乗っかっている\(X\)を考えます)

まず(1)について、和が\(180°\)となる対角を\(\angle B,\angle D\)とする。
\(△ABC\)の外接円を\(O\)とし、この円周上に\(X\)を直線\(AC\)について\(D\)と同じ側にとる。すると内接四角形\(ABCX\)について
\(\angle B+\angle AXC=180°\)・・・①
また条件より
\(\angle B+\angle D=180°\)・・・②
①②より
\(\angle AXC=\angle D\)
よって円周角の定理の逆より\(D\)も円\(O\)の周上にあるので、四角形\(ABCD\)は円に内接する。

(2)については、1内角\(α\)が対角の外角に等しいので、対角は\(180°-α\)。よって対角の和は
\(α+(180°-α)=180°\)
となり(1)と同じ条件になる。よって同様に証明できる。

 

 

 

(例題)
\(△ABC\)の外接円周上の点\(P\)から\(BC,CA,AB\)またはその延長上におろした垂線の足を\(D,E,F\)とする。

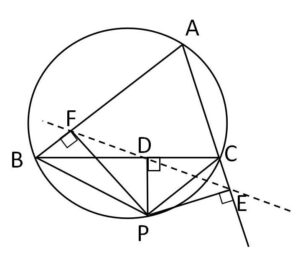
(1)\(\angle BPF=\angle CPE\) を示せ。
(2)3点\(D,E,F\)は同一直線上にあることを証明せよ。(この直線をシムソン線という)

 

(1)

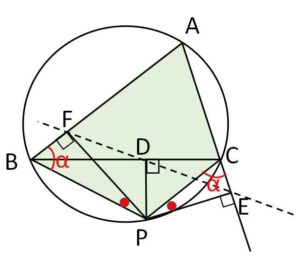
四角形\(ABPC\)は円に内接しているから
\(\angle FBP=\angle ECP=α\)
よって
\(\angle BPF=\angle CPE\ (=90°-α)\)

(2)

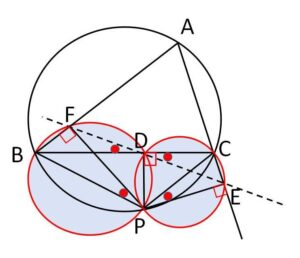
円周角の定理の逆より\(B,F,D,P\)は同一円周上にあり、また対角の和が\(180°\)であることから\(D,P,E,C\)は同一円周上にある。
よってそれぞれの円で円周角の定理を用いると
\(\angle BPF=\angle FDB\)・・・①
\(\angle CPE=\angle CDE\)・・・②

①②と(1)の結果
\(\angle BPF=\angle CPE\)
より
\(\angle FDB=\angle CDE\)
\(B,D,C\)が一直線上にあることから・・・(注)
3点\(D,E,F\)は同一直線上にある。

(注)
単に角度が等しいだけだと同一直線上にあるとは言い切れません(下図)。

 

 

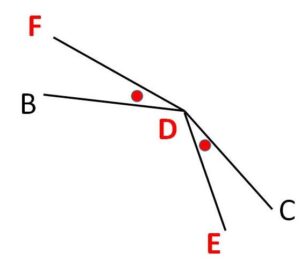
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→内接円と接線の長さ　back→円の接線