接する複数の円についてです。
・接する複数の円
円が複数接している場合も、2円の場合と同じです。2円の接点は2円の中心を結ぶ直線上にあることに着目して、直角三角形で三平方の定理を利用するのが基本です。結局、円の中心を結ぶ直線をはじめとする直線図形に最終的には着目することになり、そうすると元々の円はオサラバです。
1つだけ有名な図で考えてみます。
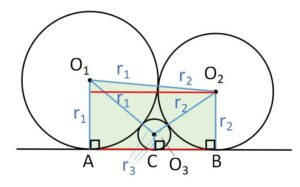
上図において、円\(O_1,O_2\)は外接しており共通接線は\(AB\)で、共通接線との接点は\(A,B\)である。さらに円\(O_3\)は円\(O_1,O_2\)に外接しており、線分\(AB\)にも接している。円\(O_1,O_2,O_3\)の半径を\(r_1,r_2,r_3\)として、これらの半径について成り立つ式を考えてみます。
まず、円\(O_1,O_2\)については共通接線\(AB\)の長さは
\(AB=\sqrt{(r_1+r_2)^2-(r_1-r_2)^2}\)
\(=2\sqrt{r_1r_2}\)
同様に円\(O_1,O_3\)、\(O_2,O_3\)においても
\(AC=2\sqrt{r_1r_3}\)
\(CB=2\sqrt{r_2r_3}\)
したがって
\(AC+CB=AB\) より
\(2\sqrt{r_1r_3}+2\sqrt{r_2r_3}=2\sqrt{r_1r_2}\)
両辺を\(2\sqrt{r_1r_2r_3}\)で割って、和の順番をいれかえると
\(\displaystyle\frac{1}{\sqrt{r_1}}+\displaystyle\frac{1}{\sqrt{r_2}}=\displaystyle\frac{1}{\sqrt{r_3}}\)
(例題)
\(C_1,C_2,C_3\)は、半径がそれぞれ\(2a,a,a\)の円とする。いま、半径\(1\)の円\(C\)にこれらが内接していて、\(C_1,C_2,C_3\)は互いに外接しているとき、\(a\)の値を求めよ。
(解答)
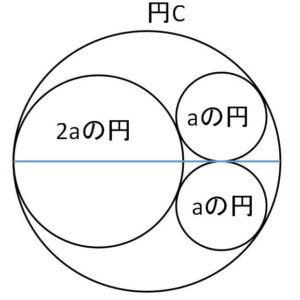
\(a\)の方程式を立てて求めることになりますが、
(i)円\(C\)と\(2a\)の円
(ii)円\(C\)と\(a\)の円
(iii)\(2a\)の円と\(a\)の円
(iv)\(a\)の円と\(a\)の円
どうしに着目します。もちろん中心を結ぶ直線を考えますが、\(a\)の円の接点がポイントです。
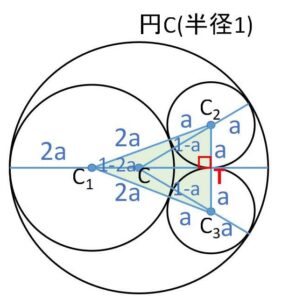
円\(C_2,C_3\)の接点を\(T\)とおくと、\(T\)は線分\(C_2C_3\)の中点。
\(△CC_2C_3\)は二等辺三角形なので、\(CT\)は\(C_2C_3\)と垂直で、同様に\(C_1T\)も\(C_2C_3\)に垂直。よって\(C_1,C,T\)は一直線上にあり、この直線は円\(C_2,C_3\)の共通内接線。
ここで
\(CT=\sqrt{(1-a)^2-a^2}\)
\(=\sqrt{1-2a}\)
\(C_1T=\sqrt{(3a)^2-a^2}\)
\(=2\sqrt{2}a\)
だから \(C_1T=CT+CC_1\) より
\(2\sqrt{2}a=\sqrt{1-2a}+(1-2a)\)・・・①
①の各項は正にならないといけないので
\(0<a<\displaystyle\frac{1}{2}\)・・・②
①より
\(2(1+\sqrt{2})a-1=\sqrt{1-2a}\)・・・③
③の右辺は正の値だから、
\(a>\displaystyle\frac{1}{2(1+\sqrt{2})}=\displaystyle\frac{-1+\sqrt{2}}{2}\)・・・④
であり、③を2乗して
\(\{2(1+\sqrt{2})a-1\}^2=1-2a\)
整理すると
\(a\{2(3+2\sqrt{2})a-(1+2\sqrt{2})\}=0\)
\(a≠0\)だから
\(a=\displaystyle\frac{1+2\sqrt{2}}{2(3+2\sqrt{2})}\)
\(=\displaystyle\frac{(1+2\sqrt{2})(3-2\sqrt{2})}{2\cdot1}\)
\(=\displaystyle\frac{-5+4\sqrt{2}}{2}\) (②④を満たす)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→軌跡・領域 back→共通接線の長さ