オイラーの定理(内心と外心の距離の定理)です。
・オイラーの定理(内心と外心の距離)
オイラーの定理という名前の定理は複数ありますが、ここでは内心と外心の距離に関する定理を扱います。別名チャップルの定理とも呼ばれます。
\(△ABC\)の外心を\(O\)、内心を\(I\)とし、外接円と内接円の半径を\(R,r\)とする。このとき
\(OI^2=R^2-2Rr\)
さらにこの等式より
\(R≧2r\) (オイラーの不等式)
(証明)
やや複雑なので3stepに分けて証明したいと思います。
(step1)\(DB=DI\)(二等辺三角形の発見)
(step2)\(AI\cdot DI=2Rr\) (正弦定理と三角比の利用)
(step3)\(OI^2=R^2-2Rr\) (方べきの定理の利用)
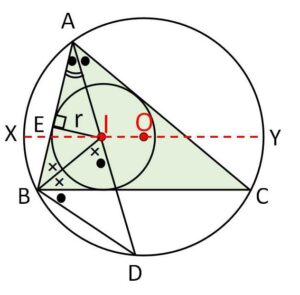
図で、\(D\)は\(AI\)の延長と外接円の交点、\(E\)は\(AB\)上の内接円の接点、\(XY\)は\(I\)を通る外接円の直径である。
(step1)\(DB=DI\) (二等辺三角形の発見)
\(I\)は\(△ABC\)の内角の二等分線の交点であることと、円周角の定理、三角形の2内角の和=残りの外角より、\(△DBI\)は二等辺三角形。よって \(DB=DI\)。
(step2)\(AI\cdot DI=2Rr\) (正弦定理と三角比の利用)
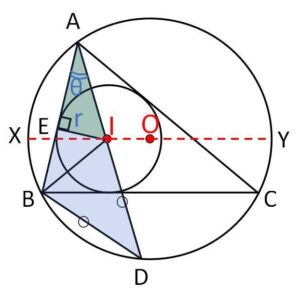
(外接円の半径\(R\)と結びつけるために正弦定理を利用)
\(\angle BAD=θ\) とおくと、\(△ABD\)において正弦定理より
\(\displaystyle\frac{DB}{\sinθ}=2R\)
(step1)より
\(\displaystyle\frac{DI}{\sinθ}=2R\)・・・①
また、\(△AEI\)は直角三角形だから
\(\sinθ=\displaystyle\frac{r}{AI}\)・・・②
①×② より
\(AI\cdot DI=2Rr\)
(step3)\(OI^2=R^2-2Rr\) (方べきの定理の利用)
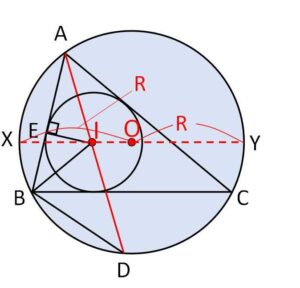
\(I\)について、\(AD,XY\)で方べきの定理より
\(AI \cdot DI=IX\cdot IY\)
(step2) と図より
\(2Rr=(R-OI)(R+OI)\)
整理すると
\(OI^2=R^2-2Rr\)
となり、内心と外心の距離を、外接円・内接円の半径より求める式が得らえる。
さらに\(OI^2≧0\)だから
\(R(R-2r)≧0\)
\(R>0\) より
\(R≧2r\) (オイラーの不等式)
となり、内接円と外接円の半径の大小関係の不等式が得られる。
等号成立は\(△ABC\)が正三角形のときであるが、これを導くには別途三角関数などの処理が必要になります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間図形の基本(2直線) back→軌跡・領域