最後に1変数関数ですが、分数関数の最大最小値についてみていきます。
(問題)
次の関数のとりうる値の範囲を求めよ。
(1) \(y=\displaystyle\frac{1}{x^2+2x+3}\)
(2) \(y=\displaystyle\frac{8x+4}{x^2-2x+5}\)
微分(数Ⅲ)しても解けますが、2次関数の知識の範囲で解いてみます。
(解答)
(1)
\(y=\displaystyle\frac{1}{x^2+2x+3}=\displaystyle\frac{1}{(x+1)^2+2}\)
(1)
\(y=\displaystyle\frac{1}{x^2+2x+3}=\displaystyle\frac{1}{(x+1)^2+2}\)
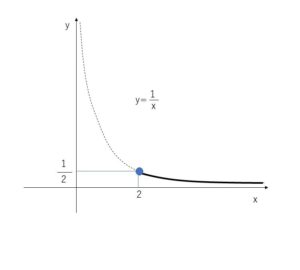
ここで \((x+1)^2+2≧2\)。また、\(y=\displaystyle\frac{1}{x}\)のグラフを考えると \(x≧2\)のとき \(0<y≦\displaystyle\frac{1}{2}\) より
求める値の範囲は \(0<y≦\displaystyle\frac{1}{2}\)
求める値の範囲は \(0<y≦\displaystyle\frac{1}{2}\)
(2)
\(y\)が\(k\)という値をとりうるとして、\(y=k\)とおいて実数解をもつ条件を考えます。\(x\)を動かす、つまり出発点を\(x\)にするのではなく、出発点を\(y\)、つまり「\(y\)がある値をとりうる」とします。
\(x^2-2x+5=(x-1)^2+4>0\)
\(y=k\)とおくと、\(k=\displaystyle\frac{8x+4}{x^2-2x+5}\)
\(y=k\)とおくと、\(k=\displaystyle\frac{8x+4}{x^2-2x+5}\)
両辺に \(x^2-2x+5≠0\) を掛けて
\(k(x^2-2x+5)=8x+4\)
整理すると
\(kx^2-2(k+4)x+5k-4=0\)・・・①
\(k(x^2-2x+5)=8x+4\)
整理すると
\(kx^2-2(k+4)x+5k-4=0\)・・・①
①が実数解\(x\)をもつ条件を考えると
(ア)\(k≠0\)のとき
\(\displaystyle\frac{D}{4}=(k+4)^2-k(5k-4)≧0\)
よって \(k^2-3k-4≦0\) これを解くと \(-1≦k≦4\)
したがって \(-1≦k≦4\) かつ \(k≠0\)
(ア)\(k≠0\)のとき
\(\displaystyle\frac{D}{4}=(k+4)^2-k(5k-4)≧0\)
よって \(k^2-3k-4≦0\) これを解くと \(-1≦k≦4\)
したがって \(-1≦k≦4\) かつ \(k≠0\)
(イ)\(k=0\)のとき
①は \(-8x-4=0\) で 実数解が存在する。
①は \(-8x-4=0\) で 実数解が存在する。
以上(ア)(イ)から \(-1≦k≦4\) すなわち \(-1≦y≦4\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。