立体の体積比についてです。
・立体の体積比
立体の体積比を求めるには次のことを利用するのが基本です。
(1)同じ高さ→底面積の比
(2)同じ底面→高さの比(別の線分比から求める)
(3)相似比の利用→3乗比が体積比
または適宜分割して直接体積を求めることもあります。
(例題1)
三角錐\(OABC\)があり、\(OA=OB=OC=2\)、\(BC=CA=AB=1\) とする。辺\(OB,OC\)上にそれぞれ \(OP=OQ=\displaystyle\frac{3}{2}\) となるように点\(P,Q\)をとるとき、三角錐\(OAPQ\)の体積\(V_1\)と元の三角錐\(OABC\)の体積\(V\)の比の値を求めよ。
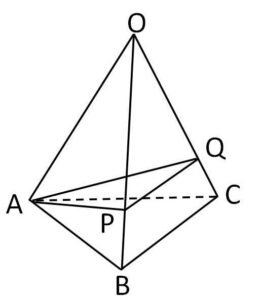
(解答)
(2)同じ底面→高さの比
を利用します。解答では(1)のみでやりますが、(2)を混ぜて二段階で考えても構いません。
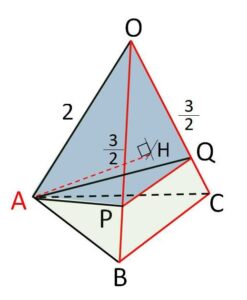
\(A\)から平面\(OBC\)に垂線\(AH\)を下ろすと、2つの三角錐は高さが\(AH\)で共通なので
\(\displaystyle\frac{V_1}{V}=\displaystyle\frac{\displaystyle\frac{3}{2}\cdot\displaystyle\frac{3}{2}}{2\cdot2}=\)\(\displaystyle\frac{9}{16}\)
(参考)
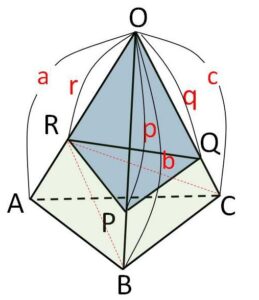
図のように\(a,b,c\)、\(p,q,r\)を線分の長さまたは、各辺における線分の長さの比とする。このとき三角錐\(OPQR\)の体積\(V_1\)と元の三角錐\(OABC\)の体積\(V\)の比は、まず\(R\)からの高さを共通として
\(V_1=\displaystyle\frac{pq}{bc}\cdot(三角錐ROBC)\)
続いて\(B\)からの高さを共通として
\((三角錐ROBC)=\displaystyle\frac{r}{a}V\)
よって
\(V_1=\displaystyle\frac{pqr}{abc}V\) (\(\displaystyle\frac{V_1}{V}=\displaystyle\frac{pqr}{abc}\))
なお四角錐では同様のことは成り立たたないので、これを利用する場合は分割して三角錐に分けることになります。
(例題2)
(1)図1のような、底面が直角二等辺三角形である三角柱がある。\(AB=AC=6\) であり、\(G,H\)はそれぞれ辺\(AB,AC\)を\(1:2\)に内分する点で、三角柱の高さは\(9\)である。このとき、\(BCEFGH\)を頂点とする立体の体積を求めよ。
(2)図2のような正四角錐がある。底面は一辺の長さが\(8\)の正方形で、\(PA=PB=PC=PD=12\) である。\(M,N\)が辺\(PA,PD\)の中点であるとき、面\(MNCB\)の上側にある部分の立体の体積を求めよ。
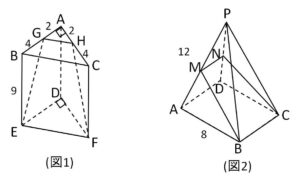
(解答)
(1)
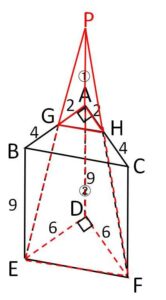
\(GE\)と\(AD\)の延長の交点を\(P\)とすると、\(AG:DE=1:3\) より
\(PA:AD=1:2\)・・・①
同様に、\(HF\)と\(AD\)の延長の交点を\(P’\)とすれば
\(P’A:AD=1:2\)
となるので\(P,P’\)は一致し、\(GE,HF,AD\)の延長は1点\(P\)で交わることになる。
三角錐\(PAGH\)と三角錐\(PDEF\)の相似比は\(1:3\)で、後者の高さは①より
\(9×\displaystyle\frac{3}{2}=\displaystyle\frac{27}{2}\)
であり、立体\(AGHDEF\)の体積は2つの三角錐の体積比が\(1:27\)であることから
\(\displaystyle\frac{1}{3}\cdot(\displaystyle\frac{1}{2}\cdot6^2)\cdot\displaystyle\frac{27}{2}\cdot(1-\displaystyle\frac{1}{27})\)
\(=78\)・・・②
したがって求める体積\(V\)は、三角柱の体積から②を除くことで
\(V=\displaystyle\frac{1}{2}\cdot6^2\cdot9-78=\)\(84\)
(2)
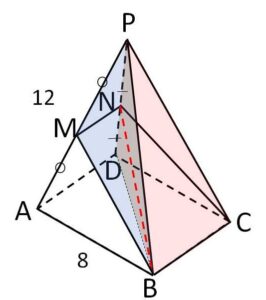
平面\(PDB\)で分割する。正四角錐\(PABCD\)の体積を\(v\)とすると
(三角錐\(PMNB\))\(=\displaystyle\frac{v}{2}\cdot\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{2}=\displaystyle\frac{v}{8}\)
(三角錐\(PNBC\))\(=\displaystyle\frac{v}{2}\cdot\displaystyle\frac{1}{2}=\displaystyle\frac{v}{4}\)
よって求める体積\(V\)は
\(V=\displaystyle\frac{v}{8}+\displaystyle\frac{v}{4}=\displaystyle\frac{3}{8}v\)
ここで正四角錐の高さは、底面の正方形の対角線の長さの半分が\(4\sqrt{2}\)より
\(\sqrt{12^2-(4\sqrt{2})^2}=4\sqrt{7}\)
となるから
\(v=\displaystyle\frac{1}{3}\cdot8^2\cdot4\sqrt{7}\)
したがって
\(V=\displaystyle\frac{3}{8}\cdot\displaystyle\frac{1}{3}\cdot8^2\cdot4\sqrt{7}\)
\(=32\sqrt{7}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→回転体 back→対称性のある立体