三角比を利用して測量の問題を解いてみます。
(問題)
ある建物の高さを測るため、その建物から\(10m\)離れた地点で高さ\(1.5m\)の位置から建物の上端\(P\)の仰角を測ったところ\(65°\)であった。\(tan65°=2.1445\)として、建物の高さを求めよ。ただし\(1m\)未満を四捨五入せよ。
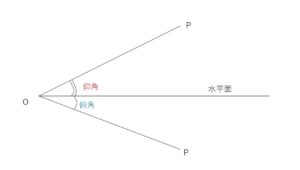
図で点Oから点Pをみるとき、OPと水平面のなす角をPがOを通る水平面より上側にあるならば仰角(ぎょうかく)、下側にあるならば俯角(ふかく)とよびます。
(解答)
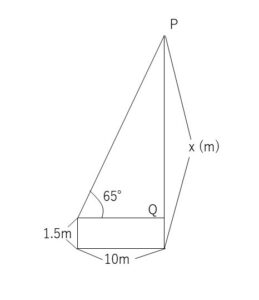
建物の高さを\(xm\)とする。下図より
\(PQ=x-1.5\)・・・①
また \(PQ=10tan65°\)・・・②
①②より \(x=1.5+10tan65°=1.5+21.445=22.945≒23\)
(答)\(23m\)
②は 三角比の定義から導くことができます。
\(\displaystyle\frac{PQ}{10}=tan65°\) の両辺に\(10\)を掛けると、\(PQ=10tan65°\)
\(\displaystyle\frac{PQ}{10}=tan65°\) の両辺に\(10\)を掛けると、\(PQ=10tan65°\)
同様に下図の三角形について以下の公式が成り立ちます。
\(a=c\) \(sinθ\)
\(b=c\) \(cosθ\)
\(a=b\) \(tanθ\)
これらは定義より導かれますが、瞬時に出せるように公式として覚えてしまった方がよいです。図と対応させて覚えましょう。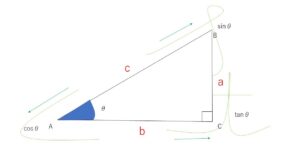
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。