・さまざまな数、\(0, 3, 5.7, -6, \sqrt{2}, \displaystyle \frac{3}{4} , \displaystyle \frac{2}{3}\)にはどんな相違点や類似点があるでしょうか。
・有理数
整数\(m\)と\(0\)でない整数\(n\)を用いて、\(\displaystyle \frac{m}{n}\)と表すことができる数を有理数といいます。整数\(m\)は、\(\displaystyle \frac{m}{1}\)と表されるので有理数です。整数でない有理数を小数で表すと、\(\displaystyle \frac{1}{4}=0.25\) のように有限個の数字で表される有限小数か、\(\displaystyle \frac{5}{3}=1.66666・・・\)のように循環小数(同じ数の並びが繰り返される無限小数)のどちらかとなります。
\(\displaystyle \frac{m}{n}\)を小数で表すには\(n\)で割る操作を繰り返すことになります。途中で割り切れたときは有限小数となり、いつまでも割り切れないときは無限小数となりますが、\(n\)で割った余りは、\( 1 ~ (n-1) \)のいずれかなのでいつかは同じ余りを\(n\)で割ることになるので循環小数となります。
分数を小数に表すのは分子を分母で割ればいいだけなので簡単です。その逆の操作(小数を分数に表す)を例題を通して見ていきましょう。
(例題)
(1)\(6.35\) (2)\(3.\dot{2}\dot{4}\)
(1)は簡単ですね。\(6.35=\displaystyle \frac{635}{100}=\displaystyle \frac{127}{20}\)
(2)は2桁ずつ数が繰り返されているので、\(x=3.\dot{2}\dot{4}\)とおいて \(100x\) と \(x\) の差を考えましょう。
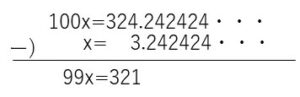
よって\(x=\displaystyle \frac{321}{99}=\displaystyle \frac{107}{33}\)
(2)は2桁ずつ数が繰り返されているので、\(x=3.\dot{2}\dot{4}\)とおいて \(100x\) と \(x\) の差を考えましょう。
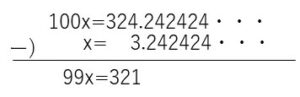
よって\(x=\displaystyle \frac{321}{99}=\displaystyle \frac{107}{33}\)
以上の例からも分かりますが、有限小数、循環小数で表される数は有理数となります。
また、2つの有理数の和、差、積、商も有理数であることもおさえておきましょう。
・無理数
有理数でない数を無理数といいます。整数・有限小数・循環小数(以上分数で表されるもの)は有理数なので、循環しない無限小数が無理数ということになります。
(例)\(\sqrt{2}=1.41421356・・・, \pi=3.141592・・・\) など
有理数でない数を無理数といいます。整数・有限小数・循環小数(以上分数で表されるもの)は有理数なので、循環しない無限小数が無理数ということになります。
(例)\(\sqrt{2}=1.41421356・・・, \pi=3.141592・・・\) など
・実数
整数、有限小数、無限小数で表される数を実数といいます。つまり実数は有理数と無理数をあわせたものです。
整数、有限小数、無限小数で表される数を実数といいます。つまり実数は有理数と無理数をあわせたものです。
実数についても有理数と同様、2つの実数の和、差、積、商もまた実数となることをおさえておきましょう。
(まとめ)
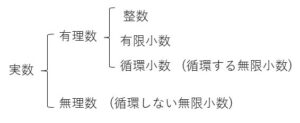
以上になります。お疲れさまでした。
ここまで読んで下さりありがとうございました。