正弦定理や余弦定理を利用して、与えられたもの以外の三角形の辺と角を決定していきます。正弦定理・余弦定理をそれぞれ利用した今までも同じことをやっているのですが、答えが2個ある場合や1個しかない場合がありました。その解の個数の目安を正弦定理・余弦定理の長所や短所を交えて考えていきます。
(例題1)
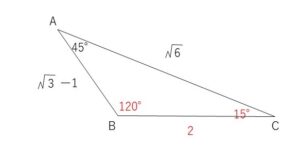
\(△ABC\)において、\(b=\sqrt{6},c=\sqrt{3}-1,A=45°\) のとき、\(a,B,C\)を求めよ。
(解法1)余弦定理のみを利用する場合
\(a^2=(\sqrt{6})^2+(\sqrt{3}-1)^2-2\sqrt{6}(\sqrt{3}-1)\cos45°=4\)
\(a>0\) だから \(a=2\)
また、\(\cos B=\displaystyle\frac{(\sqrt{3}-1)^2+2^2-(\sqrt{6})^2}{2・(\sqrt{3}-1)・2}=-\displaystyle\frac{1}{2}\)
\(0°<B<180°-45°\) だから、\(B=120°\)
したがって、\(C=180°-(45°+120°)=\)\(15°\)
(解法2)余弦定理と正弦定理を両方使う場合
\(a^2=(\sqrt{6})^2+(\sqrt{3}-1)^2-2\sqrt{6}(\sqrt{3}-1)\cos45°=4\)
\(a>0\) だから \(a=2\)
正弦定理より、\(\displaystyle\frac{2}{\sin45°}=\displaystyle\frac{\sqrt{6}}{\sin B}\)
\(\sin B=\displaystyle\frac{\sqrt{3}}{2}\)
\(0°<B<180°-45°\) だから、\(B=60°,120°\)
\(B=60°\) のとき \(C=75°\)
\(B=120°\) のとき \(C=15°\)
※辺と角の大小関係については (→(3-6)三角形の成立条件と辺と角の大小関係) を参照してください。辺の大小関係とその対角の大小関係は一致するので、最も小さい辺の対角が最も大きい角ではおかしいということです。
(例題2)
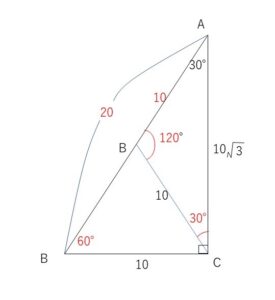
\(△ABC\)において、\(a=10,b=10\sqrt{3},A=30°\) のとき、\(c,B,C\)を求めよ。
図を描いてみて判断します。
余弦定理より
\(10^2=(10\sqrt{3})^2+c^2-2・10\sqrt{3}・c・\cos 30°\)
整理すると
\(c^2-30c+200=0\) \((c-10)(c-20)=0\) より
\(c=10,20\)
\(a=c=10\) の二等辺三角形なので、\(B=120°,C=30°\)
\(\cos B=\displaystyle\frac{20^2+10^2-(10\sqrt{3})^2}{2・20・10}=\displaystyle\frac{1}{2}\)
\(0°<B<180°-30°\) だから \(B=60°\)
よって、\(C=180°-(30°+60°)=90°\)
①②を合わせた図は下の通りです。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。