整式の計算は、高校数学で最初に習う分野で、定期試験などで出題されることはあっても、そのものが入試で問われることは少ないでしょう。ですが、高校数学のあらゆる分野で必要となってくるまさに土台のようなものなので、しっかり身につけましょう。計算結果が答えと合わない場合はどこで計算ミスをしたか確認して、答えと合うまで練習を積み重ねましょう。
整式の加法・減法・乗法では、次の法則を利用して計算します。
交換法則
\(A+B=B+A\) \(AB=BA\)
結合法則
\((A+B)+C=A+(B+C)\) \((AB)C=A(BC)\)
分配法則
\(A(B+C)=AB+AC\) \((A+B)C=AC+BC\)
\(A+B=B+A\) \(AB=BA\)
結合法則
\((A+B)+C=A+(B+C)\) \((AB)C=A(BC)\)
分配法則
\(A(B+C)=AB+AC\) \((A+B)C=AC+BC\)
一番重要なのは分配法則です。整式を展開する際に何度も使用します。交換法則と結合法則は簡単に言えば、計算をする順番を入れ替えてもよいという法則です。何を当たり前のことを言っているんだと思う方もいるかもしれませんが、分野によっては成り立たない場合があります。例えば、行列の積やベクトルの外積(いずれも高校数学範囲外)は交換法則が必ずしも成り立ちません。
指数法則
\(m,n\)を正の整数とすると、
①\(a^ma^n=a^{m+n}\) ②\((a^m)^n=a^{mn}\)
③\((ab)^m=a^mb^m\)
\(m,n\)を正の整数とすると、
①\(a^ma^n=a^{m+n}\) ②\((a^m)^n=a^{mn}\)
③\((ab)^m=a^mb^m\)
指数の計算は、和なのか積なのか間違えやすいところです。\(m,n\)に具体的な数値を代入して考えてみましょう。
①\(a^3a^4=(aaa)(aaaa)=a^{3+4}=a^7\)
\((≠a^{3×4})\)
\((≠a^{3×4})\)
②\((a^3)^4=(aaa)(aaa)(aaa)(aaa)=a^{3×4}=a^{12}\)
\((≠a^{3+4})\)
\((≠a^{3+4})\)
ちなみに、\(a^{3^4}=a^{81}\) \(≠(a^3)^4\)となります。
整式の展開
整式の積を計算して整理した形にすることを、整式の展開といいます。
例) \((x+2)(x+3)\)
\(=(x+2)x+(x+2)3\)
\(=x^2+2x+3x+6\)
\(=x^2+5x+6\)
\(=(x+2)x+(x+2)3\)
\(=x^2+2x+3x+6\)
\(=x^2+5x+6\)
\((a+b+1)(a+2b)\)
\(=(a+b+1)a+(a+b+1)2b\)
\(=a^2+ab+a+2ab+2b^2+2b\)
\(=a^2+3ab+a+2b^2+2b\)
\(=(a+b+1)a+(a+b+1)2b\)
\(=a^2+ab+a+2ab+2b^2+2b\)
\(=a^2+3ab+a+2b^2+2b\)
上記記載の分配法則等を使って計算しています。整式を整理する際には、同類項(例では\(2x\)と\(3x\)、\(ab\)と\(2ab\))をまとめることを忘れずに。
※一般に整式の積\(P×Q\)を展開するには、\(P\)の1つ1つの項に\(Q\)の各項をもれなく重複なく掛けて加えればよいです。
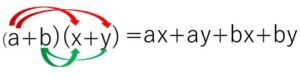
(\(P=a+b, Q=x+y\))
分配法則等を使って整式を整理すれば時間はかかりますが、どんな複雑な式でも計算できます。しかし当たり前ですが、複雑になればなるほど手間もかかりますし、計算ミスもずっと増えることでしょう。なので展開する際には工夫がとても重要になってきます。次回以降工夫を見ていきましょう。
以上です。お疲れさまでした。
ここまで見て頂いてありがとうございました。