空間図形の測量問題について考えていきます。部分的に平面図形を考えれば、基本的には平面図形の測量の問題とやることは変わりません。
(問題)
ある山の頂上\(A\)の高さを知るために、下の図のように、同一平面上で\(500m\)離れた2地点\(P,Q\)から水平角や仰角を測ったところ、\(\angle APB=30°,\angle BPQ=105°,\angle BQP=45°\) であった。このとき山の高さ\(AB\)を求めよ。
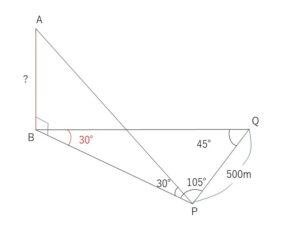
2つの三角形を別々に考えます。まずは水平面上での\(△BPQ\)について、1辺と2角(内角の和が180°よりもう1つの角も決定)が分かっているので、正弦定理より、\(BP\)を求めます。あとは鉛直面上での\(△ABP\)が直角三角形だから、\(AB=BP\tan30°\)です。
(解答)
\(\angle PBQ=180°-(45°+105°)=30°\) だから
\(△BPQ\)において正弦定理より
\(\displaystyle\frac{BP}{\sin45°}=\displaystyle\frac{500}{\sin30°}\)
よって \(BP=500\sqrt{2}\)
また、\(△ABP\)は\(\angle PBA=90°\)の直角三角形だから
\(AB=BP\tan30°=500\sqrt{2}・\displaystyle\frac{1}{\sqrt{3}}\)\(=\)\(\displaystyle\frac{500\sqrt{6}}{3}(m)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。