今までは、1つの変量\(x\)についてのデータの分析をしてきましたが、今回からは2つの変量\(x,y\)が対になったデータの分析について学んでいきます。
・散布図
2つの変量\(x,y\)を対にした\(n\)個のデータを、\((x_1,y_1),(x_2,y_2),・・・(x_{n},y_{n})\)とするとき、これらの分析のため\(xy\)座標平面に\(n\)個の点として表示します。表示された図を散布図とよびます。
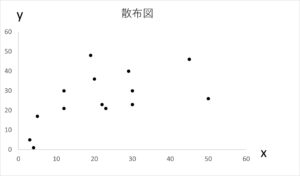
例えば、あるクラス40人の英語と数学のテストの点数の分析の場合、\(x\)軸に英語の点数、\(y\)軸に数学の点数をとり40個の点を打ちます。この2つのテストの点数にどんな関係があるのかをグラフから読み取ろうと考えるわけです。
・相関関係
2つの変量の間に、一方が増えると他方も増える(または一方が減ると他方も減る)関係があるとき2つの変量の間に正の相関があるといい、一方が増えると他方は減る(または一方が減ると他方が増える)関係があるとき2つの変量の間に負の相関があるといいます。どちらの関係もみられないときは相関がないといいます。
2つの変量の間に、一方が増えると他方も増える(または一方が減ると他方も減る)関係があるとき2つの変量の間に正の相関があるといい、一方が増えると他方は減る(または一方が減ると他方が増える)関係があるとき2つの変量の間に負の相関があるといいます。どちらの関係もみられないときは相関がないといいます。
正の相関の例は「勉強時間が増えるほどテストの点数が上がる」や「身長が高い人ほど体重が重い」、負の相関の例は「駅から遠いほどマンションの家賃が安い」や「運動時間が長いほど体重が落ちる」などでしょうか。(あくまでも例なので場合によっては違うこともあります)
相関関係は直線的な関係について考えます。散布図の点が直線的に広がっているかどうかで判断するか(次項解説)、相関係数(→(2-5)相関係数 参照)により判断します。
・相関関係と散布図
2つの変量に正の相関があるとき、散布図の点の分布は右上がりの直線に近く、負の相関があるときは点の分布が右下がりの直線に近くなります。また、より直線的な傾向が強い場合はそれぞれ正の相関が強い、負の相関が強いといいます。相関関係がないときは直線上に分布していないことになります。
2つの変量に正の相関があるとき、散布図の点の分布は右上がりの直線に近く、負の相関があるときは点の分布が右下がりの直線に近くなります。また、より直線的な傾向が強い場合はそれぞれ正の相関が強い、負の相関が強いといいます。相関関係がないときは直線上に分布していないことになります。
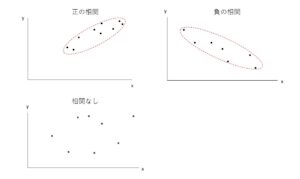
直線上に点が分布してない場合は何も特徴がないデータということではありません。散布図上の点がある関数の曲線上にあるなど他の特徴がある場合もあります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。