集合の分野の知識は、場合の数・確率・命題など多数の分野で必要なものなのでしっかりとおさえておきましょう。
・集合とその要素
範囲がはっきりとしたものの集まりを集合といいます。例えば、「1から10までの偶数の集まり」といったら範囲がはっきりとしていますが、「大きい数の集まり」といっても範囲がはっきりしていないので集合ではありません。ある集合を表すときは\(A,B\)などの大文字を使って表します。
また、集合を作っている1つ1つのものをその集合の要素または元(げん)といいます。
集合\(A\)を「1から10までの偶数の集まり」とした場合、要素を使って集合\(A\)を表す方法は次のような方法があります。
(1)要素を書き並べて表す方法
\(A=\{2,4,6,8,10\}\)
(2)要素の条件を示す方法
\(A=\{2n|n\)は整数\(,1≦n≦5\}\) など
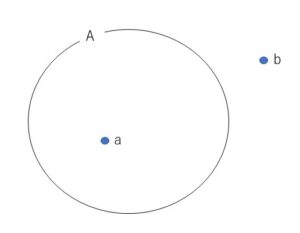
\(a\)が集合\(A\)の要素であるとき、\(a\)は集合\(A\)に属するといい記号で次のように表します。
\(a\in A\) または \(A\ni a\)
また、\(b\)が集合\(A\)の要素でないことを
\(b\notin A\) または \(A\not\ni b\)
と表します。
これらを図で表すと次のようになり、このような図をベン図とよびます。
・部分集合
2つの集合\(A,B\)が例えば、\(A=\{1,3,5\}\),\(B=\{1,2,3,4,5\}\)のような場合であるとき、\(A\)のどの要素も\(B\)の要素となっています。このような場合、\(A\)を\(B\)の部分集合といい、\(A\)は\(B\)に含まれる、または\(B\)は\(A\)を含むといい、
\(A\subset B\) または \(B\supset A\)
と表します。
\(A\)のどの要素も\(B\)の要素となっているので、\(x\in A\) ならば、\(x\in B\)が成り立ちます。
これらのことをベン図で表すと次のようになります。
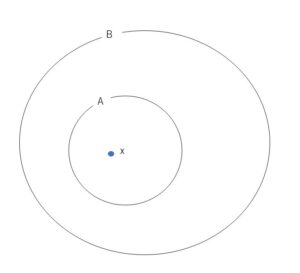
なお、\(A\)のどの要素も\(A\)の要素となるので、\(A\)自身も\(A\)の部分集合となります。
また、\(A \subset B\) かつ \(B \subset A\)が成り立つとき、\(A,B\)の要素がすべて一致し、\(A=B\) と表します。
以上になります。お疲れ様でした。
ここまで見ていただきありがとうございました。