今まで2つの集合について考えてきましたが、今回は3つの集合について考えていきます。
・3つの集合の共通部分と和集合
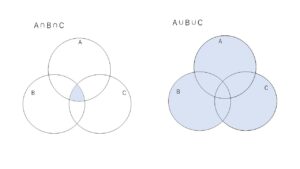
2つの集合の場合と同じように、3つの集合\(A,B,C\)のどれにも属する要素全体の集合を、\(A,B,C\)の共通部分といい、\(A \cap B \cap C\) と表します。また、\(A,B,C\)の少なくとも1つに属する要素全体の集合を、\(A,B,C\)の和集合といい、\(A \cup B \cup C\)と表します。ベン図で表すと次のとおりです。
(例題)
\(20\)以下の自然数全体を全体集合とし、奇数、\(3\)の倍数、\(5\)の倍数の集合を、それぞれ\(A,B,C\)とする。このとき次の集合を求めよ。
(1)\((A \cap C) \cup (B \cap C)\)
(2)\((A \cup C) \cap (B \cup C)\)
(3)\(\overline{A \cup B \cup C}\)
(解答)
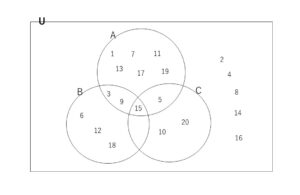
\(A=\{1,3,5,7,9\)\(,11,13,15,17,19\}\)
\(B=\{3,6,9,12,15,18\}\)
\(C=\{5,10,15,20\}\)
であり、
\(A \cap B=\{3,9,15\}\), \(A \cap C=\{5,15\}\), \(B \cap C=\{15\}\), \(A \cap B \cap C=\{15\}\) だから、ベン図は次のとおり。
(1)
\(A \cap C=\{5,15\}\), \(B \cap C=\{15\}\), だから
\((A \cap C) \cup (B \cap C)=\)\(\{5,15\}\)
(2)
\(A \cup C=\)\(\{1,3,5,7,9,10\)\(,13,15,17,19,20\}\)
\(B \cup C=\)\(\{3,5,6,9,10\)\(,12,15,18,20\}\) だから
\((A \cup C) \cap (B \cup C)=\)\(\{3,5,9,10,15,20\}\)
(3)
ベン図より
\(\overline{A \cup B \cup C}=\)\(\{2,4,8,14,16\}\)
・交換法則と結合法則と分配法則
3つの集合\(A,B,C\)についてベン図を考えると以下の法則が成り立つことがわかります。
\(A \cap B=B \cap A\), \(A \cup B=B \cup A\)
②結合法則
\((A \cap B) \cap C\)\(=A \cap (B \cap C)\)\(=A \cap B \cap C\)
\((A \cup B) \cup C\)\(=A \cup (B \cup C)\)\(=A \cup B \cup C\)
③分配法則
\((A \cup B) \cap C\)\(=(A \cap C) \cup (B \cap C)\)
\((A \cap B) \cup C\)\(=(A \cup C) \cap (B \cup C)\)
3つの集合について次の式が成り立ちます。(ド・モルガンの法則の拡張)
\(\overline{A \cup B \cup C}\)\(=\overline A \cap \overline B \cap \overline C\)
(証明)
(\(A \cap B\)) と \(C\)、2つの集合の場合を考えると、ド・モルガンの法則により、
\(\overline{A \cap B \cap C}\)\(=\overline{(A \cap B) \cap C}\)\(=\overline{(A \cap B)} \cup \overline C\)\(=(\overline A \cup \overline B) \cup \overline C\)\(=\overline A \cup \overline B \cup \overline C\)
2つ目の式は \(\cap\) と\(\cup\) を入れ替えれば得られる。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。