円順列とじゅず順列

それでは異なる5個の玉の円順列の総数はどうなるでしょうか。
次の図の5個の円形の並び方は、すべて時計回りの並び順が色1,2,3,4,5の順番になっていて、これら5個の並び方は回転させると重なるので、円順列としては同じものになります。

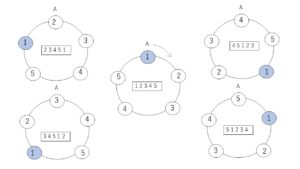
一番上にある場所を\(A\)として、時計回りに普通の順列を考えると図の5個の並び方は、12345,23451,34512,45123,51234, となります。この5つの順列の両端を結ぶと円順列としては同じものができるので、普通の順列では区別されていた5個のものが円順列では同じものとして扱われることになります。

これ以外の円形の並び方でも同じで、1つの円順列に対して5つの順列があることになるので、

円順列の総数は
\(5!÷5=4!=(5-1)!\)(通り)
となります。

また、別の考え方でも円順列の総数を求めることができます。
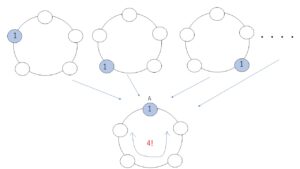
回転できるままで考えると難しいので、色1を一番上の\(A\)の位置に固定します。(すべての円順列の色1を一番上にもってくる)
そして、残りの色2,3,4,5の順列の総数は \(4!\)通りとなり、これら\(4!\)通りの円順列は回転させても自分自身にしか重ならないため、別々のものとなります。よって、円順列の総数は　\(4!=(5-1)!\)通り です。

一般的に\(n\)個の場合でも同じように考えると

・じゅず順列
異なる5個の玉を糸につないで輪にすると、次の図の2つのものは裏返すと同じになります。いくつかのものを糸でつないで輪にして、回転や裏返しして一致するものは同じものとみるとき、その並び方をじゅず順列といいます。

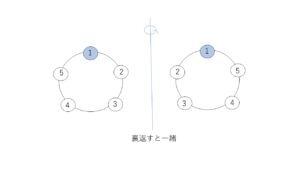
円順列のなかには裏返すと一緒になるものが2つずつあるので、じゅず順列の総数は円順列の半分となります。

(例題)

7個の異なる宝石がある。
(1)これらを机の上に環状に並べる方法は何通りあるか。
(2)これらの宝石で首飾りを作ると何通りのものができるか。
(3)7個の宝石のうち5個を選んで机の上に環状に並べる方法は何通りあるか。

(解答)
(1)
7個の異なるものの円順列の総数だから
\((7-1)!=6!=\)\(720\)(通り)

(2)
7個の異なるもののじゅず順列の総数だから
\((7-1)!÷2=\)\(360\)(通り)

(3)
異なる7個から5個とる順列の総数\({}_7\mathrm{P}_5\)には、円順列としては同じものが5個ずつあるので
\({}_7\mathrm{P}_5÷5=(7・6・5・4・3)÷5=\)\(504\)(通り)