平面に色を塗る方法の場合の数を求める問題について考えます。
(問題)
次の図の\(A,B,C,D,E\)各領域を色分けしたい。隣り合った領域には異なる色を用い、指定された数だけの色は全部用いなければならない。塗り分け方はそれぞれ何通りか。
(1)5色を用いる場合
(2)4色を用いる場合
(3)3色を用いる場合
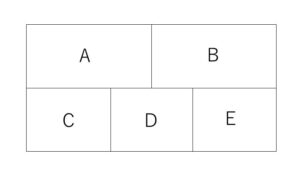
複雑な場合には樹形図を考えるのも有効です。
(解答)
(1)
5色を用いる場合は、どう塗っても同じ色が隣り合うことはない。
5色の塗り分け方の総数は、5色を1列に並べる方法の総数と同じなので、
\(5!=\)\(120\)(通り)
(2)
4色を、色1,2,3,4とする。
\(A,C,D\)は隣り合っているので、4色のうち3色を使うことになり、その塗り方の総数は、\({}_4\mathrm{P}_3\)(通り)。\(A,C,D\)に使った色を例えばそれぞれ色1,2,3とする。\(B\)に使用できる色は、\(C\)に使用した色2か、まだ使っていない色4で、\(E\)についても考えると樹形図は次のとおりになり、\(B,E\)の塗り方は3(通り)。
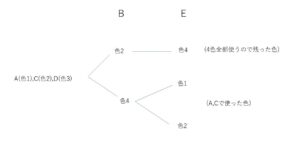
他の\(A,C,D\)の塗り方でも\(B,E\)の塗り方は同様の数あるので、求める塗り方の数は、
\({}_4\mathrm{P}_3×3=\)\(72\)(通り)
(3)
3色を色1,2,3とする。
\(A,C,D\)は隣り合っているのでこの3色をすべて使い、塗り方の総数は、\(3!\)(通り)
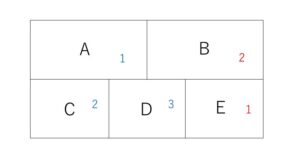
\(A,C,D\)に塗った色をそれぞれ\(1,2,3\)とすると、\(B\)は\(C\)に使った色2で塗り、\(E\)は\(B,D\)で使った色2,3でない色を使うので、色1で塗ることになり、\(B\)は色2、\(E\)は色1で塗るしかなく塗り方は1通り。他の\(A,C,D\)の塗り方でも同じように\(B,E\)の塗り方は1通りしかないので、求める塗り方の数は
\(3!×1=\)\(6\)(通り)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。