立体の色の塗り分けの問題についてみていきます。ここでは立体の面と塗る色の数が等しい場合について考えます。(立体の面より塗る色の数少ない場合は、同じ色を複数回使うので、組合せのところで扱います。)
(例題1)
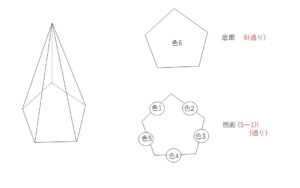
立体を回転させて一致する塗り方は同じとみなすとき、正五角錐の各面を異なる6色すべてを使って塗る方法は何通りあるか。
正五角錐の側面はすべて合同な二等辺三角形です。
横方向に回転させると、他の面があった場所にぴったり重ね合わせることができるので、円順列の考え方を利用します。
横方向に回転させると、他の面があった場所にぴったり重ね合わせることができるので、円順列の考え方を利用します。
(解答)
底面に塗る色の選び方は、6通り。
その各々に対して、側面の塗り方は、底面以外の5色の円順列を考えると \((5-1)!\)通りある。よって
\(6×4!=\)\(144\)(通り)
(例題2)
立方体の各面に、隣り合った面の色は異なるように、色を塗りたい。ただし立方体を回転させて一致する塗り方は同じとみなす。このとき、異なる6色をすべて使って塗る方法は何通りあるか。
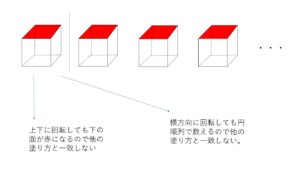
今度は立方体なので上下方向に回転しても他の面のあった場所に重なります。
こういった立体(立方体や正四面体など)の塗り分けの時は、ある1つの色の面を一番上に固定し、まず上下方向の回転をおさえます。あとは下の面と横の面の塗り分けをします。横方向はさらにまだ回転できるため、円順列の数え方を使います。
こういった立体(立方体や正四面体など)の塗り分けの時は、ある1つの色の面を一番上に固定し、まず上下方向の回転をおさえます。あとは下の面と横の面の塗り分けをします。横方向はさらにまだ回転できるため、円順列の数え方を使います。
6色を、赤・青・黄・緑・茶・黒とします。
ここでいう固定とは、赤色なら赤色と特定の色を決めてしまうことです。まず赤で固定したから、次は青で・・・とはしません。すべての塗り方に赤色の面が存在するので、それぞれの塗り方について赤色の面を一番上に持ってくるわけです。こうしてあとは下の面と横の面(円順列を考える)の塗り方を\(x\)通りを数えてやれば、\(x\)通りのそれぞれの塗り方は、回転しても自分自身にしか重ならないため別々の塗り方になります。
ここでいう固定とは、赤色なら赤色と特定の色を決めてしまうことです。まず赤で固定したから、次は青で・・・とはしません。すべての塗り方に赤色の面が存在するので、それぞれの塗り方について赤色の面を一番上に持ってくるわけです。こうしてあとは下の面と横の面(円順列を考える)の塗り方を\(x\)通りを数えてやれば、\(x\)通りのそれぞれの塗り方は、回転しても自分自身にしか重ならないため別々の塗り方になります。
(解答)
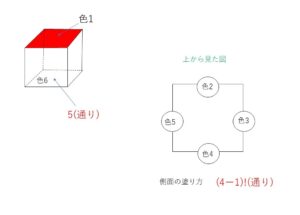
6色を色1,2,3,4,5,6とする。
上の面を色1で塗り固定すると、下の面は残り5色のうち1つ選ぶから、5通り。
この各々について側面の塗り方は、残り4色の円順列を考えると、\((4-1)!\) 通りある。
よって塗り方の総数は \(5×3!=\)\(30\)(通り)
(例題3)
正五角柱の7つの面を、異なる7色をすべて使って塗り分ける方法は何通りあるか。ただし正五角柱を回転したり倒したりして同じになる塗り方は1通りとする。
この立体も上下左右に回転させて他の面があった場所に重ねることができますが、立方体と違って、側面と上面・底面が違います。よって上面をある1色で固定することができません。(側面に赤色を使った場合、上面に赤色をもってくることができない)
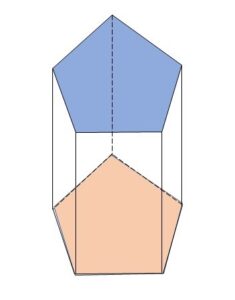
この場合、横方向は円順列の考えを使うとして、問題は上面と底面です。上面と底面を区別しないまま(立体を上下方向に回転できるまま)だと難しいので、上面と底面をひとまず区別することにします。要は色を固定するのではなく、立体自体を固定します。そして、最後に重複して数えた分(上面と底面を回転させて入れ替えて同じになる分)を調整します。

この場合、横方向は円順列の考えを使うとして、問題は上面と底面です。上面と底面を区別しないまま(立体を上下方向に回転できるまま)だと難しいので、上面と底面をひとまず区別することにします。要は色を固定するのではなく、立体自体を固定します。そして、最後に重複して数えた分(上面と底面を回転させて入れ替えて同じになる分)を調整します。
(解答)
正五角柱の上面と底面を区別すると、正五角柱の上面の塗り方は7通り、底面の色の塗り方は6通り。側面の塗り方は残り5色の円順列を考えると \((5-1)!\)通りで、全部で\(7×6×(5-1)!\)(通り)
このうち、上面と底面の色が逆で、側面の色の並び方が右回りと左回りで同じものは回転させて上面と底面を入れ替えると一致するので、上面と底面を区別した塗り方それぞれには同じものが2つずつ含まれている。
よって、求める数は
\(7×6×(5-1)!÷2=\)\(504\)(通り)
正五角柱の上面と底面を区別すると、正五角柱の上面の塗り方は7通り、底面の色の塗り方は6通り。側面の塗り方は残り5色の円順列を考えると \((5-1)!\)通りで、全部で\(7×6×(5-1)!\)(通り)
このうち、上面と底面の色が逆で、側面の色の並び方が右回りと左回りで同じものは回転させて上面と底面を入れ替えると一致するので、上面と底面を区別した塗り方それぞれには同じものが2つずつ含まれている。
よって、求める数は
\(7×6×(5-1)!÷2=\)\(504\)(通り)
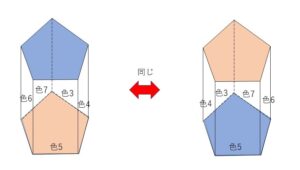
最後に2で割るのは、じゅず順列の考え方です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。