整数解の個数問題を重複組合せの考えを使って解いていきます。
(例題)
(1)\(x+y+z=8\), \(x≧0\), \(y≧0\), \(z≧0\) を満たす、整数 \(x,y,z\) の組 \((x,y,z)\)は、全部で何組あるか。
(2)\(x+y+z=8\) を満たす、正の整数\(x,y,z\) の組 \((x,y,z)\)は、全部で何組あるか。
(3)\(x+y+z≦8\), \(x≧0\), \(y≧0\), \(z≧0\) を満たす、整数 \(x,y,z\) の組 \((x,y,z)\)は、全部で何組あるか。
今回の例題のケースでは0以上の整数や自然数といった条件があるために解の個数が限られてきます。
(1)
8個の数字1を、\(x,y,z\)に分配すると考える。
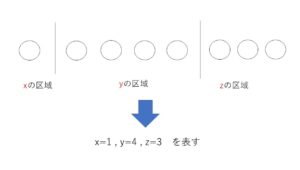
数字1を〇として8個の〇と、仕切り2個を並べる。
仕切りで分けられた領域を、左から\(x,y,z\)の領域として、各領域にある〇の数が各文字における方程式の解であるとする。8個の〇と、仕切り2個の並べ方の総数が解の組の総数となるので、
\({}_{10}\mathrm{C}_8=\)\(45\)(組)
解の組は、異なる3つの文字\(x,y,z\)から重複を許して8個選ぶ重複組合せを考えることになります。
\(x+y+z=8\), \(x≧1\), \(y≧1\), \(z≧1\) を満たす、整数 \(x,y,z\) の組 \((x,y,z)\)は、全部で何組あるか
ということになります。
(1)のように0以上の整数という条件にするために、
\(x-1=X\), \(y-1=Y\), \(z-1=Z\) と置き換えます。
\(x≧1\), \(y≧1\), \(z≧1\) より、
\(X≧0\), \(Y≧0\), \(Z≧0\)・・・②
①を変形して、\(x+y+z=8\)に代入すると
\((X+1)+(Y+1)+(Z+1)=8\) となり
\(X+Y+Z=5\)・・・③
②③を満たす\(X,Y,Z\)の組の個数は、もとの\(x,y,z\)の組の個数と等しいので、求める組の個数は、(1)と同様に考えると、5個の〇と2個のしきりの並べ方の総数で
\({}_7\mathrm{C}_5=\)\(21\)(組)
(3)
\(x+y+z=0,1,2,3,\)\(4,5,6,7,8\) なので
9通りすべて組の数を考えて和をとっても答えは出ますが、
解答ではスマートに求める方法でやってみたいと思います。
\(w=8-(x+y+z)\) とすると、\(x+y+z≦8\)より、\(w≧0\)となり
\(x+y+z+w=x+y+z+8-(x+y+z)=8\) と等式にもちこむことができて
\(x+y+z+w=8\) \((x≧0,y≧0,\)\(z≧0,w≧0)\)
の解の組を求めればよいことになります。
\(w=8,7,6,5,\)\(4,3,2,1,0\) が上の \(x+y+z=0,1,2,3,\)\(4,5,6,7,8\) に対応しています。
\(w=8-(x+y+z)\) とすると、\(x+y+z≦8\)より、\(w≧0\)となり
\(x+y+z+w=8\) \((x≧0,y≧0,\)\(z≧0,w≧0)\)・・・(A)
(A)を満たす \((x,y,z,w)\)の組は全部で、〇8個と仕切り3つの並び方を考えて
\({}_{11}\mathrm{C}_8=165\)(組)
これら165個の\((x,y,z,w)\)の組は、\(x+y+z≦8\)を満たすので、求める\(x,y,z\) の組も \(165\)(組)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。