基本性質・加法定理・和事象の確率

確率について成り立つ基本性質や定理について学んでいきます。

・確率の基本性質
ある試行において、その全事象を\(U\)、その中にある事象を\(A\)とすると、\(P\)を確率として、次の性質が成り立ちます。

\(0≦P(A)≦1\)
特に
\(P(φ)=0\),　\(P(U)=1\)

確率は0から1の間の数値になります。

(証明)
\(0≦n(A)≦n(U)\) だから、すべての辺を\(n(U)\)で割って、
\(0≦\displaystyle\frac{n(A)}{n(U)}≦1\)
つまり
\(0≦P(A)≦1\)

特に

\(A\)が空事象\(φ\)のとき、\(n(A)=0\) だから、\(P(A)=P(φ)=0\)
\(A\)が全事象\(U\)のとき、\(P(A)=P(U)=\displaystyle\frac{n(U)}{n(U)}=1\)

・積事象と和事象
1個のさいころを投げる試行において、
「偶数の目が出る」という事象を\(A\)、「4以下の目が出る」という事象を\(B\)とすると、
これらは
\(A=\{2,4,6\}\),　\(B=\{1,2,3,4\}\)　と表されます。

このとき「偶数の目が出る　かつ　4以下の目が出る」という事象は、\(A\)と\(B\)の共通部分
\(A \cap B=\{2,4\}\)
で表され、

「偶数の目が出る　または　4以下の目が出る」という事象は、\(A\)と\(B\)の和集合
\(A \cup B=\{1,2,3,4,6\}\)
で表されます。

一般に、全事象\(U\)の中の2つの事象を\(A,B\)とすると、
「事象\(A\)と\(B\)がともに起こる」という事象を、\(A\)と\(B\)の積事象といい、\(A \cap B\) で表し

「事象\(A\)または\(B\)が起こる」という事象を、\(A\)と\(B\)の和事象といい、\(A \cup B\) で表します。

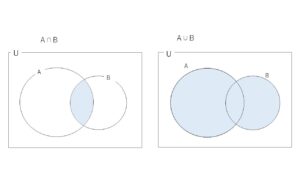
積事象 \(A \cap B\)、和事象 \(A \cup B\) は、それぞれ1個のサイコロを投げる例のように集合で表すと
共通部分\(A \cap B\), 和集合\(A \cup B\) として表されます。
和事象　積事象

・和事象の確率と加法定理
2つの事象A,Bについて、和事象\(A \cup B\)の確率を考えます。
それぞれの事象(集合)の要素の数について

\(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)

が成り立つので、両辺\(n(U)\)で割ると

\(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)

が成り立ちます。

とくに、事象\(A\)と事象\(B\)が同時には決して起こらないとき、つまり
\(A \cap B=φ\)
のとき、事象\(A\)と事象\(B\)は互いに排反である、または互いに排反事象であるといい、
\(P(A \cap B)=P(φ)=0\) だから

\(P(A \cup B)=P(A)+P(B)\) (加法定理)

となります。

AとBが同時に起こらない場合は単純に足すだけです。
AとBが同時に起こることがある場合は積事象の確率を引くことになります。
集合の要素の個数のときと似たようなイメージです。

また、3つ以上の事象については、その中のどの2つの事象も互いに排反であるとき、これらの事象は互いに排反である、または互いに排反事象であるといい、次の加法定理が成り立ちます。

\(P(A \cup B \cup C \cup・・・)\)\(=P(A)+P(B)+P(C)+・・・\)

(例題)
2つの組A,Bがあって、各組は次のように構成されている。
A組:男子2人、女子3人　B組:男子4人、女子1人
この2つの組を合わせた10人の生徒から任意に3人の委員を選ぶとき
(1)3人の委員の中にいずれの組の女子生徒も含まれる確率を求めよ。
(2)3人の委員がB組の生徒だけになるか、または男子生徒だけになる場合の確率を求めよ。

排反か排反でないかに注意します。

(解答)
(1)

B組の女子は必ず選ばれます。
A組の女子から最低1人選ぶことになるので、
(ア)A組の女子から1人のみ選ぶ　(イ)A組の女子から2人選ぶ
場合で分けます。(ア)(イ)は同時に起こることはないので排反です。

B組の女子は必ず委員に選ばれる。残り2人の委員のうち1人はA組の女子から選ばれるので
(ア)A組の女子から1人選び、男子6人から1人選ぶ
(イ)A組の女子から2人選ぶ
場合が考えられる。(ア)(イ)は互いに排反となるので、求める確率は

\(\displaystyle\frac{{}_3\mathrm{C}_1×{}_6\mathrm{C}_1+{}_3\mathrm{C}_2}{{}_{10}\mathrm{C}_3}=\)\(\displaystyle\frac{7}{40}\)

(2)

委員がB組の生徒のみになる事象をM、男子のみになる事象をNとします。
M,Nは排反ではありません。M \(\cap\) N、つまりB組の男子のみになる場合があるからです。

委員がB組の生徒だけになる事象をM、男子だけになる事象をNとする。
\(P(M)=\displaystyle\frac{{}_{5}\mathrm{C}_3}{{}_{10}\mathrm{C}_3}\)

\(P(N)=\displaystyle\frac{{}_{6}\mathrm{C}_3}{{}_{10}\mathrm{C}_3}\)

\(P(M \cap N)=\displaystyle\frac{{}_{4}\mathrm{C}_3}{{}_{10}\mathrm{C}_3}\)

だから、求める確率は

\(P(M \cup N)=P(M)+P(N)-P(M \cap N)\)
\(=\displaystyle\frac{{}_{5}\mathrm{C}_3}{{}_{10}\mathrm{C}_3}+\displaystyle\frac{{}_{6}\mathrm{C}_3}{{}_{10}\mathrm{C}_3}-\displaystyle\frac{{}_{4}\mathrm{C}_3}{{}_{10}\mathrm{C}_3}\)

\(=\displaystyle\frac{10+20-4}{{}_{10}\mathrm{C}_3}\)

\(=\)\(\displaystyle\frac{13}{60}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
→高校数学TOP　next→余事象の確率　 back→格子点と確率