確率の乗法定理に関する問題を見ていきます。
(例題)
袋の中に最初赤玉2個と青玉1個が入っている。次の操作を考える。
(操作)
「袋から1個の玉を取り出し、それが赤玉ならば代わりに青玉1個を袋に入れ、青玉ならば代わりに赤玉1個を袋に入れる。袋に入っている3個の玉がすべて青玉になるとき、硬貨を1個もらう。」
この操作を4回繰り返す。もらう硬貨の総数が1枚である確率と、もらう硬貨の総数が2枚である確率をそれぞれ求めよ。
(解答)
考えられる、袋に入っている赤玉と青玉の個数は
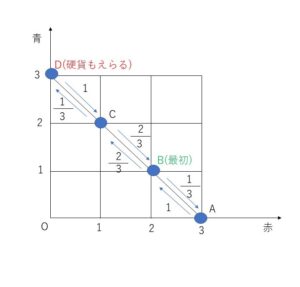
(赤,青)=A(3,0),B(2,1),C(1,2),D(0,3) の4通り。
また図のように、座標平面上にA,B,C,Dをとり、各状態に推移する確率を示すと次の通り。
まず、硬貨の総数が1枚である確率を考える。
最初、Bの位置の状態にあり、4回推移していくうち1回だけDの状態に推移すればよいので、
①B→C→D→C→B
②B→C→B→C→D
③B→A→B→C→D
の場合がある。それぞれの確率は
①\(\displaystyle\frac{2}{3}・\displaystyle\frac{1}{3}・1・\displaystyle\frac{2}{3}\)\(=\displaystyle\frac{4}{27}\)
②\(\displaystyle\frac{2}{3}・\displaystyle\frac{2}{3}・\displaystyle\frac{2}{3}・\displaystyle\frac{1}{3}\)\(=\displaystyle\frac{8}{81}\)
③\(\displaystyle\frac{1}{3}・1・\displaystyle\frac{2}{3}・\displaystyle\frac{1}{3}\)\(=\displaystyle\frac{2}{27}\)
であり、それぞれ排反なので求める確率は
\(\displaystyle\frac{4}{27}+\displaystyle\frac{8}{81}+\displaystyle\frac{2}{27}=\)\(\displaystyle\frac{26}{81}\)
次に硬貨の総数が2枚のときを考えると
B→C→D→C→D
と推移する場合だけなので、求める確率は
\(\displaystyle\frac{2}{3}・\displaystyle\frac{1}{3}・1・\displaystyle\frac{1}{3}=\)\(\displaystyle\frac{2}{27}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。