\(n\)進法に関する数列の問題を見ていきます。
(例題)
\(0,1,2,3\) の4種類で表される自然数を、\(1\)桁から\(4\)桁まで小さい順に並べると、
\(1,2,3,10,11\)\(,12,13,20,21\)\(,22・・・\)
となる。
(1)\(3103\)は何番目の数か。
(2)\(150\)番目の数は何か。
(3)整数は全部で何個並ぶか。
小さい順から\(10\)進数で番号を\(1,2,3,4,5・・・\)とつけていきます。
問題の数字を\(4\)進数の列とみて、これらを\(10\)進法で表すと、つけた番号と一致します。

問題の数字を\(4\)進数の列とみて、これらを\(10\)進法で表すと、つけた番号と一致します。

(解答)
(1)
\(3103_{(4)}\)を\(10\)進数に直せばよいことになります。
問題の数列は\(10\)進数の列、\(1,2,3,4,・・・\)を\(4\)進数で表したものである。
よって、\(3103_{(4)}\)を\(10\)進数にすると
\(3103_{(4)}=3・4^3+1・4^2+0・4^1+3=211\)
したがって\(3103\)は\(211\)番目の数である。
(2)
(1)とは逆に、\(10\)進数 \(150\) を\(4\)進数にすればよいことになります。
\(150\)を\(4\)進数に直すと
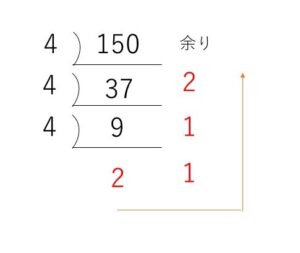
\(150=2112_{(4)}\) となるので
\(150\)番目の数は、\(2112\)
(3)
数列の最後の数は、\(4\)桁で最も大きい数(\(4\)進法の数)です。
それは\(3333\)です。\(3333\)が何番目にあるかが分かれば、その数が並んででいる数字の個数の総数です。
それは\(3333\)です。\(3333\)が何番目にあるかが分かれば、その数が並んででいる数字の個数の総数です。
数列の最後の数は\(3333\)であり、\(3333_{(4)}\)を\(10\)進数にすると
\(3333_{(4)}=3・4^3+3・4^2+3・4+3=255\)
よって\(3333\)は\(255\)番目の数であるから
並んでいる整数は全部で \(255\)(個)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。