ガウス記号・ガウス記号を含む関数

→高校数学TOP

今回からガウス記号について学んでいきます。
まずはガウス記号の定義から始めます。

・ガウス記号

(例)
\([2.4]=2\),　\([5]=5\),　\([\sqrt{3}]=1\),　\([-3.4]=-4\)  (\(-3\)ではない)
など。
\([5]\)は\(5\)を超えない最大の整数なので、\([5]=5\)です。(\(5\)だとギリギリ超えていません)

・ガウス記号の性質

(解説)
①\([x]\)は整数です。定義より当たり前ですが、強く意識するようにしてください。

②例えば\([2.4]\)について数直線で考えてみます。

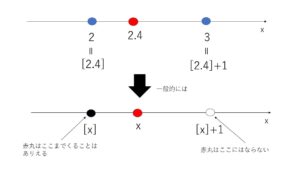
図より、\([2.4]<2.4<[2.4]+1\) となります。
これを一般化すると、
\([x]≦x<[x]+1\)
となります。左側の等号が成立するときは、\(x\)が整数のときです。

③　②を変形すると得られます。

④数直線を考えると次の通り。

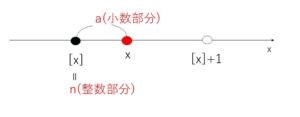
よって、\(x=n+a=[x]+a\)
\([x]\)が\(x\)の整数部分で、\(x-[x]\)が小数部分となります。

⑤ざっくりと説明すると、左側のガウス記号では、\(x,y\)がそれぞれ小数部分がカットされるが、右側は和をとったあとカットされる。小数部分の和が\(1\)を超えることがあるので、右側のほうが大きくなることがあるということです。

丁寧にやると

\([x]≦x<[x]+1\),　\([y]≦y<[y]+1\) より辺々足して
\([x]+[y]≦x+y<[x]+[y]+2\)

よって
\([x+y]=[x]+[y]\) or \([x]+[y]+1\)
したがって、\([x]+[y]≦[x+y]\)

⑥\(x\)に整数を足しても、小数部分には影響がありません。よって整数\(k\)を足してからガウス記号をとっても、ガウス記号をとってから\(k\)を足しても同じです。

丁寧にやると
\([x]≦x<[x]+1\) より、両辺に整数\(k\)を加えて
\([x]+k≦x+k<[x]+k+1\)

よって \([x+k]=[x]+k\)

⑦やや発展的な内容ですが、\(x\)を例えば、\(0.4,0.5,0.6\) とすると
\([2x]\)については
\([2(0.4)]=[0.8]=0\)
\([2(0.5)]=[1]=1\)
\([2(0.6)]=[1.2]=1\) であり

\([x+\displaystyle\frac{1}{2}]\)については
\([0.4+\displaystyle\frac{1}{2}]=[0.4+0.5]=0\)
\([0.5+\displaystyle\frac{1}{2}]=[0.5+0.5]=1\)
\([0.6+\displaystyle\frac{1}{2}]=[0.6+0.5]=1\)

となり、\(x\)の小数部分が\(0.5\)となるところが境目になります。
また、\([x]\)と\([2x]\)については、小数部分が\(0\)、つまり\(x\)が整数となるところが境目になるので、全体としては\(0.5\)刻みで場合分けすればよさそうです。

(証明)
\(m\)を整数とすると、

(ア)\(m≦x<m+\displaystyle\frac{1}{2}\)・・・(1) のとき

\([x]=m\)

また、(1)より
\(m+\displaystyle\frac{1}{2}≦x+\displaystyle\frac{1}{2}<m+1\) だから
\([x+\displaystyle\frac{1}{2}]=m\)

さらに(1)より \(2m≦2x<2m+1\) なので
\([2x]=2m\)

よって、\([2x]=[x]+[x+\displaystyle\frac{1}{2}]\) が成り立つ。

(イ)\(m+\displaystyle\frac{1}{2}≦x<m+1\)・・(2) のとき
\([x]=m\)

また(2)より
\(m+1≦x+\displaystyle\frac{1}{2}<m+1+\displaystyle\frac{1}{2}\) だから
\([x+\displaystyle\frac{1}{2}]=m+1\)

さらに(2)より \(2m+1≦2x<2m+2\) なので
\([2x]=2m+1\)

よって、\([2x]=[x]+[x+\displaystyle\frac{1}{2}]\) が成り立つ。

以上より任意の実数\(x\)について等式が成り立つ。

・ガウス記号を含む関数
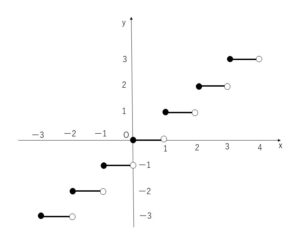
\(y=[x]\) のグラフはどのようになるかを考えてみます。

具体的に範囲を区切って考えてみると、

\(-2≦x<-1\)   のとき \(y=[x]=-2\)
\(-1≦x<0\)      のとき \(y=[x]=-1\)
\(0≦x<1\)         のとき \(y=[x]=0\)
\(1≦x<2\)         のとき \(y=[x]=1\)
\(2≦x<3\)　　　のとき \(y=[x]=2\)
となり、規則性よりグラフを描くと次の通りです。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→ガウス記号の例題①　back→n進法と数列