ガウス記号の例題①

→高校数学TOP

ガウス記号に関する問題について見ていきます。

(例題1)
実数\(x\)に対して\(x\)以下の最大の整数を\([x]\)で表す。
(1)\([\displaystyle\frac{1}{3}x+1]=-2\) を満たす\(x\)の範囲を求めよ。
(2)\([\displaystyle\frac{1}{6}x]=[\displaystyle\frac{1}{2}x+1]\) を満たす\(x\)の範囲を求めよ。

(解答)
(1)

\(-2≦\displaystyle\frac{1}{3}x+1<-1\) より
\(-3≦\displaystyle\frac{1}{3}x<-2\)
よって
\(-9≦x<-6\)

(2)

\([\displaystyle\frac{1}{6}x]=[\displaystyle\frac{1}{2}x+1]=k\)　(\(k\)は整数) とおける。

\([\displaystyle\frac{1}{6}x]=k\)より
\(k≦\displaystyle\frac{1}{6}x<k+1\)
よって
\(6k≦x<6k+6\)・・・①

また、\([\displaystyle\frac{1}{2}x+1]=k\) より
\(k≦\displaystyle\frac{1}{2}x+1<k+1\) だから

\(2k-2≦x<2k\)・・・②

①と②の共通解があれば、方程式の解があることになるので、①②が共通解をもつ条件を調べる。

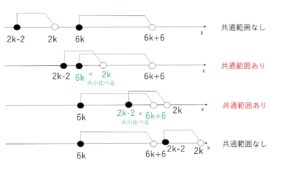
①②が共通の範囲をもつときは
\(6k<2k\) かつ \(2k-2<6k+6\)
これを解くと、\(-2<k<0\)
\(k\)は整数なので、\(k=-1\)

\(k=-1\)を①②に代入して
\(-6≦x<0\)・・・③,　\(-4≦x<-2\)・・・④
よって求める\(x\)の範囲は③④の共通範囲で
\(-4≦x<-2\)

(例題2)
実数\(x\)に対して\(k≦x<k+1\) を満たす整数\(k\)を\([x]\)で表す。
(1)\(n^2-n-\displaystyle\frac{5}{4}<0\) を満たす整数\(n\)をすべて求めよ。
(2)\([x]^2-[x]-\displaystyle\frac{5}{4}<0\) を満たす実数\(x\)の範囲を求めよ。
(3)\(x\)は(2)で求めた範囲にあるものとする。\(x^2-[x]-\displaystyle\frac{5}{4}=0\) を満たす\(x\)をすべて求めよ。

(解答)
(1)

\(n^2-n-\displaystyle\frac{5}{4}=0\)を解くと
\(n=\displaystyle\frac{1±\sqrt{6}}{2}\)

よって、不等式を満たす\(n\)は
\(\displaystyle\frac{1-\sqrt{6}}{2}<n<\displaystyle\frac{1+\sqrt{6}}{2}\)・・・①

\(2<\sqrt{6}<3\) より
\(-1<\displaystyle\frac{1-\sqrt{6}}{2}<-\displaystyle\frac{1}{2}\)
\(\displaystyle\frac{3}{2}<\displaystyle\frac{1+\sqrt{6}}{2}<2\)

だから、①を満たす整数\(n\)は
\(n=0,1\)

(2)

\([x]=n\) (\(n\)は整数) とすると、(1)と同じ不等式になる。

よって\([x]=0,1\)

(ア)\([x]=0\) のとき
\(0≦x<1\)
(イ)\([x]=1\) のとき
\(1≦x<2\)

以上より \(0≦x<2\)

(3)

(i)\(0≦x<1\) のとき
\([x]=0\) なので与式は
\(x^2-\displaystyle\frac{5}{4}=0\)
これを解くと、\(x=±\displaystyle\frac{\sqrt{5}}{2}\)
\(0≦x<1\) の範囲内にないため不適。

(ii)\(1≦x<2\) のとき
\([x]=1\) なので与式は
\(x^2-1-\displaystyle\frac{5}{4}=0\)
これを解くと、\(x=±\displaystyle\frac{3}{2}\)
\(1≦x<2\) の範囲内にあるのは、\(x=\displaystyle\frac{3}{2}\)

以上より、\(x=\displaystyle\frac{3}{2}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→ガウス記号の例題②  back→ガウス記号・ガウス記号を含む関数