次の問題について考えていきます。
(例題)
次の問いに答えよ。
(1)任意の自然数\(a\)に対して、\(a^2\)を\(3\)で割った余りは\(0\)か\(1\)であることを証明せよ。
(2)自然数\(a,b,c\)が \(a^2+b^2=3c^2\) を満たすと仮定すると、\(a,b,c\)はすべて\(3\)で割り切れなければならないことを証明せよ。
(3)\(a^2+b^2=3c^2\) を満たす自然数\(a,b,c\)は存在しないことを証明せよ。
(解答)
(1)
\(k\)を整数とする。
まず、\(a=3k\)のとき
\(a^2=9k^2=3・3k^2\) より、\(a^2\)を\(3\)で割った余りは\(0\)
次に、\(a=3k±1\)のとき
\(a^2=(3k±1)^2=9k^2±6k+1\)\(=3(3k^2±2k)+1\) より
\(a^2\)を\(3\)で割った余りは\(1\)
以上より、\(a^2\)を\(3\)で割った余りは、\(0\)か\(1\)である。
(2)
\(3c^2\)は\(3\)の倍数なので、\(a^2+b^2\)も\(3\)の倍数。
\(a^2,b^2\)を\(3\)で割った余りは、\(0\)か\(1\)なので、\(a^2+b^2\)が\(3\)の倍数、つまり\(3\)で割った余りが\(0\)になるのは、\(a^2\)と\(b^2\)どちらも\(3\)で割った余りが\(0\)となる場合しかありません。
(1)より\(a^2+b^2\)を\(3\)で割った余りは次のとおり。
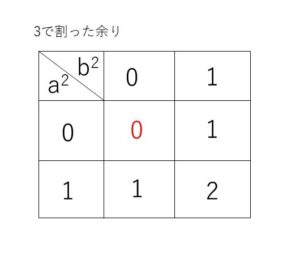
\(3c^2\)は\(3\)の倍数だから、\(a^2+b^2\)も\(3\)の倍数。
よって表より、\(a^2\)と\(b^2\)ともに\(3\)の倍数であり
\(a,b\)も\(3\)の倍数である。
ゆえに\(a=3s\) \(b=3t\) (\(s,t\)は自然数)として等式に代入すると
\(9s^2+9t^2=3c^2\)
\(3s^2+3t^2=c^2\)
左辺は\(3\)の倍数だから、\(c^2\)は\(3\)の倍数であり
\(c\)も\(3\)の倍数となる。
以上より、\(a,b,c\)はすべて\(3\)の倍数であり、題意は示された。
(3)
1つ目の解法は最小の数を設定して、それ以下の整数が存在することにより矛盾を示す解法です。
(解法1)最小数を設定する方法
\(a^2+b^2=3c^2\)・・・(A) を満たす自然数\(a,b,c\)が存在すると仮定する。
このうち最小の自然数の組を、\(a_1,b_1,c_1\)とする。
(2)より、\(a_1,b_1,c_1\)は\(3\)の倍数となるので
\(a_1=3a_2\), \(b_1=3b_2\), \(c_1=3c_2\) (\(a_2,b_2,c_2\)は自然数)
と表すことができる。
等式に代入して
\(9a_2^2+9b_2^2=3・9c_2^2\)
よって
\(a_2^2+b_2^2=3c_2^2\)・・・(B)
(B)は自然数\(a_2,b_2,c_2\)が(A)を満たすことを示している。
しかし、\(a_2<a_1\) であり、\(a_1\)が最小であることに矛盾する。
したがって、\(a^2+b^2=3c^2\)を満たす自然数\(a,b,c\)は存在しない。
(解法2)何度も\(3\)で割り切れる整数が存在することで不合理性を示す方法
\(a^2+b^2=3c^2\)・・・(A) を満たす自然数\(a,b,c\)が存在すると仮定する。
(2)より\(a,b,c\)は\(3\)の倍数となるので
\(a=3a_1\),\(b=3b_1\), \(c=3c_1\)・・・(※) となる自然数\(a_1,b_1,c_1\)が存在する。
(A)に代入して
\(9a_1^2+9b_1^2=3・9c_1^2\)
\(a_1^2+b_1^2=3c_1^2\)
よって\(a_1,b_1,c_1\)も(A)を満たすので、
\(a_1=3a_2\),\(b_1=3b_2\), \(c_1=3c_2\) となる自然数\(a_2,b_2,c_2\)が存在する。
(A)に代入して
\(9a_2^2+9b_2^2=3・9c_2^2\)
\(a_2^2+b_2^2=3c_2^2\)
ゆえに、\(a_2,b_2,c_2\)も(A)を満たす。
以下繰り返すと、(※)は、\(a_1=\displaystyle\frac{1}{3}a\), \(b_1=\displaystyle\frac{1}{3}b\), \(c_1=\displaystyle\frac{1}{3}c\) とも表せるので、\(a,b,c\)を\(3\)で割った自然数\(a_1,b_1,c_1\)が存在して(A)を満たし、さらにそれらを\(3\)で割った自然数\(a_2,b_2,c_2\)が存在して(A)を満たし、以下繰り返すと無限に\(3\)で割り切ることのできる自然数が存在することになるが、そのような自然数は存在しない。
したがって、\(a^2+b^2=3c^2\)を満たす自然数\(a,b,c\)は存在しない。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。