複数の2次方程式と判別式

複数の2次方程式と判別式に関する問題について見ていきます。

(例題1)
2次方程式
\(x^2+4ax+5-a=0\)・・・①　\(x^2+3x+3a^2=0\)・・・②
について次の条件を満たす実数の定数\(a\)の値の範囲を求めよ。
(1)①,②がどちらも実数解をもたない。
(2)①,②の一方だけが虚数解をもつ。

(解答)
(1)
①の判別式を\(D_1\)、②の判別式を\(D_2\)とする。

\(\displaystyle\frac{D_1}{4}=(2a)^2-(5-a)=4a^2+a-5\)\(=(4a+5)(a-1)\)
\(D_2=9-12a^2=-3(4a^2-3)\)\(=-3(2a+\sqrt{3})(2a-\sqrt{3})\)

①②のどちらも実数解をもたないので、
\(D_1<0\)  かつ　\(D_2<0\)

\(D_1<0\) のとき \(-\displaystyle\frac{5}{4}<a<1\)・・・(A)
\(D_2<0\) のとき \(a<-\displaystyle\frac{\sqrt{3}}{2}\) , \(a>\displaystyle\frac{\sqrt{3}}{2}\)・・・(B)

(A)(B)の共通範囲を考えると
\(-\displaystyle\frac{5}{4}<a<-\displaystyle\frac{\sqrt{3}}{2}\), 　\(\displaystyle\frac{\sqrt{3}}{2}<a<1\)

(2)

①②のどちらか一方のみが虚数解をもつには
\(D_1<0\) と \(D_2<0\)のどちらか一方のみが成り立てばよい。

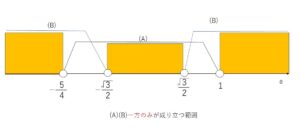
(1)の(A),(B)より数直線を考えると
\(a≦-\displaystyle\frac{5}{4}\),　\(-\displaystyle\frac{\sqrt{3}}{2}≦a≦\displaystyle\frac{\sqrt{3}}{2}\),　\(a≧1\)

(例題2)
実数\(a,b,c\)に対して次のような3つの方程式がある。
\(x^2+2ax+2b-1=0\)・・・①
\(x^2+2bx+2c-1=0\)・・・②
\(x^2+2cx+2a-1=0\)・・・③
①②③のうち、少なくとも1つは実数解をもつことを示せ。

(解答)
①②③の判別式を、\(D_1,D_2,D_3\)とする。

\(\displaystyle\frac{D_1}{4}=a^2-2b+1\)
\(\displaystyle\frac{D_2}{4}=b^2-2c+1\)
\(\displaystyle\frac{D_3}{4}=c^2-2a+1\)

よって
\(\displaystyle\frac{D_1}{4}+\displaystyle\frac{D_2}{4}+\displaystyle\frac{D_3}{4}\)
\(=(a^2-2b+1)+(b^2-2c+1)+(c^2-2a+1)\)
\(=(a^2-2a+1)+(b^2-2b+1)+(c^2-2c+1)\)
\(=(a-1)^2+(b-1)^2+(c-1)^2≧0\)・・・(C)

ここで、①～③がすべて虚数解をもつと仮定すると、\(\displaystyle\frac{D_1}{4}<0\),\(\displaystyle\frac{D_2}{4}<0\),\(\displaystyle\frac{D_3}{4}<0\)

すると、\(\displaystyle\frac{D_1}{4}+\displaystyle\frac{D_2}{4}+\displaystyle\frac{D_3}{4}<0\) となり(C)と矛盾。

したがって、①②③の少なくとも1つは実数解をもつ。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

next→虚数係数の2次方程式　back→判別式と虚数解