必要条件と十分条件

→高校数学TOP

いままで、\(p→q\)の真偽などについて考えてきましたが、\(p→q\)　(または\(q→p\) ， \(p \leftrightarrow q\))が真のとき、\(p,q\)に特別な用語が与えられます。

・必要条件・十分条件・必要十分条件(同値)
2つの条件\(p,q\)について、\(p→q\)が真のとき

\(q\) は \(p\) (であるため)の必要条件である
\(p\) は \(q\) (であるため)の十分条件である

といいます。

また、\(p\leftrightarrow q\)が真のとき、

\(p\)は\(q\)(\(p\)は\(q\))であるための必要十分条件である
また、\(p\)と\(q\)は互いに同値である

といいます。

・集合と必要・十分条件
→(6-2)命題の真偽②(集合の利用)　では、集合と命題の真偽の関係について説明しましたが、集合を考えても2つの条件\(p,q\)が十分条件なのか必要条件なのか判断することができます。条件\(p,q\)を満たす集合をそれぞれ\(P,Q\)とおくと

①について

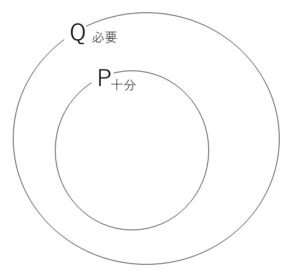
qが必要条件→Qのほうが広い(条件としてはゆるい)イメージです。

用語の使い方に慣れるまで色々な問題を解いてみて下さい。

(例題)
\(x,y\)を実数とするとき、空欄に入る語句を(ア)～(エ)の中から選べ。

(1)\(xy=0\)  であることは  \(x=0\)であるための　(      )
(2)\(xy>1\)　であることは  \(x>1\)であるための  (      )

(ア)必要条件
(イ)十分条件
(ウ)必要十分条件
(エ)必要条件でも十分条件でもない

(解答)
(1)
\(xy=0→x=0\)は偽 (反例:\(x=3,y=0\))
\(x=0→xy=0\)は真
よって (ア)必要条件

(2)
\(xy>1→x>1\)は偽　(反例:\(x=-2,y=-3\))
\(x>1→xy>1\)は偽   (反例:\(x=2,y=-3\))
よって (エ)必要条件でも十分条件でもない

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　　next→逆・裏・対偶　  back→否定②