座標を利用した証明問題について見ていきます。
(例題)
3点 \(A(1,5)\),\(B(0,1)\),\(C(5,3)\) を頂点とする\(△ABC\)の重心を\(G\)とし、\(G\)を通り2辺\(AB,AC\)(ともに両端を除く)と交わる直線を\(l\)とする。3点\(A,B,C\)と\(l\)との距離を順に\(d_1,d_2,d_3\)とするとき、\(d_1=d_2+d_3\) が成り立つことを証明せよ。
(解答)
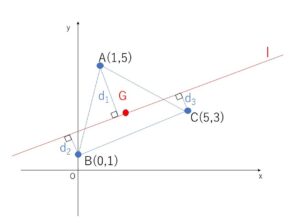
重心\(G\)の座標は
\((\displaystyle\frac{1+0+5}{3},\displaystyle\frac{5+1+3}{3})\)\(=(2,3)\)
直線\(l\)の傾きを\(m\)とおくとその方程式は
\(y-3=m(x-2)\)・・・①
2辺\(AB\),\(AC\)(両端を除く)と交わるためには、
\(GCの傾き<m<BGの傾き\)
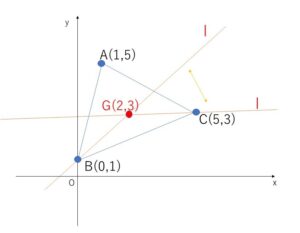
よって \(0<m<1\)
①より \(l:mx-y-2m+3=0\)
ゆえに
\(d_1=\displaystyle\frac{|m-5-2m+3|}{\sqrt{m^2+1}}\)\(=\displaystyle\frac{|-m-2|}{\sqrt{m^2+1}}\)\(=\displaystyle\frac{m+2}{\sqrt{m^2+1}}\)
\(d_2=\displaystyle\frac{|-1-2m+3|}{\sqrt{m^2+1}}\)\(=\displaystyle\frac{|-2m+2|}{\sqrt{m^2+1}}\)\(=\displaystyle\frac{-2m+2}{\sqrt{m^2+1}}\)
\(d_3=\displaystyle\frac{|5m-3-2m+3|}{\sqrt{m^2+1}}\)\(=\displaystyle\frac{|3m|}{\sqrt{m^2+1}}\)\(=\displaystyle\frac{3m}{\sqrt{m^2+1}}\)
したがって
\(d_2+d_3=\displaystyle\frac{-2m+2}{\sqrt{m^2+1}}+\displaystyle\frac{3m}{\sqrt{m^2+1}}\)\(=\displaystyle\frac{m+2}{\sqrt{m^2+1}}\)\(=d_1\) が成り立つ。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の方程式① back→直線と三角形の等分