軌跡の基礎(アポロニウスの円)

軌跡について学んでいきます。

・軌跡
定点\(O\)からの距離が一定値\(3\)であるような点\(P\)、つまり\(OP=3\)である点\(P\)の描く図形は\(O\)を中心とする半径\(3\)の円です。
このように与えられた条件を満たす点全体の集合を、その条件を満たす点の軌跡といいます。

軌跡の方程式を求める手順については次の通りです。

①②関しては、求める点\(P\)の座標を\(x,y\)などとおいて、条件を\(x,y\)で表し、そこから\(x,y\)の方程式を求める(軌跡の方程式を求める)という自然な流れなので大丈夫だと思います。
なぜ③の確認が必要なのかということは次回詳しく扱いたいと思います。

(例題)
(1)2点 \(A(-2,0)\),\(B(4,0)\) から等距離にある点\(P\)の軌跡を求めよ。
(2) (1)の\(A,B\)に対して、\(AP:BP=2:1\) を満たす点\(P\)の軌跡を求めよ。

(解答)
(1)

\(P(x,y)\)とおくと、条件より
\(AP=BP\)
\(AP>0\), \(BP>0\) より
\(AP^2=BP^2\)

よって
\((x+2)^2+y^2\)\(=(x-4)^2+y^2\)
整理すると
\(x=1\)・・・①

したがって条件を満たす点\(P\)は①上にある。

また、逆に①の上の任意の点は条件を満たす。

答 直線 \(x=1\)

(2)
\(P(x,y)\)とおくと、条件より
\(AP=2BP\)
\(AP>0\), \(BP>0\) より
\(AP^2=4BP^2\)

よって
\((x+2)^2+y^2\)\(=4\{(x-4)^2+y^2\}\)
整理すると
\(x^2-12x+y^2+20=0\)
\((x-6)^2+y^2=16\)・・・②

したがって条件を満たす点\(P\)は②上にある。

また、逆に②上の任意の点は条件を満たす。

答  円 \((x-6)^2+y^2=4^2\)

※アポロニウスの円について
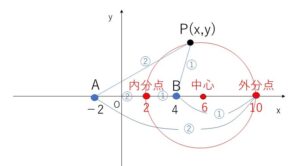
2定点 \(A,B\) からの距離の比が \(m:n\) (\(m,n>0\) \(m≠0\)) である点の軌跡は、「線分\(AB\)を\(m:n\)に内分する点と外分する点を直径の両端とする円」となり、これをアポロニウスの円といいます。なお、\(m=n\)のときの軌跡は 「線分\(AB\)の垂直二等分線」となります(例題(1))。

この性質を利用すると(2)については
\(A(-2,0)\),\(B(4,0)\) について \(AP:BP=2:1\) なので
線分\(AB\)を
\(2:1\)に内分する点は \((2,0)\)
\(2:1\)に外分する点は \((10,0)\)

よって求める軌跡は \((2,0)\),　\((10,0)\) を直径の両端とする円なので
中心はこれらの中点で \((6,0)\)、　半径は \(10-6=4\) より
円 \((x-6)^2+y^2=4^2\) となります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→軌跡と逆の確認(十分性の確認)　back→放物線と円の共有点