\(y>mx+n\) のような不等式は座標平面上では何を表すか見ていきます。
・不等式と領域(関数型)
\(y>x+2\) が表す図形について
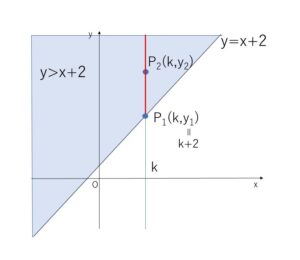
\(y=x+2\) は直線であり、この直線と\(x=k\) との交点を\(P_1(k,y_1)\) とすると、\(y_1=k+2\)・・・①
\(x=k\)上の点で\(P_1\)より上側にあるものを\(P_2(k,y_2)\)とすると、\(y_2>y_1\) であり、①より \(y_2>k+2\)
よって、\(x=k\)上については \(P_1\)より上側にある部分(領域)が\(y>x+2\) が表すものとなっています。
\(k\)を動かすと、他の\(x=k\) 上の点についても同様のことがいえるので、結局 \(y>x+2\) が表す領域は 直線\(y=x+2\) より上側の部分になります。
また同様に考えると、\(y<x+2\) が表す領域は直線 \(y=x+2\) より下側の部分になることが分かります。
以上のことを踏まえると、関数\(y=f(x)\) について
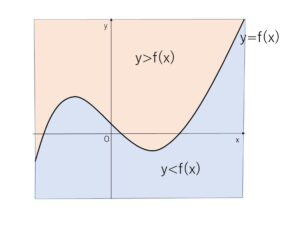
\(y>f(x)\) は 曲線 \(y=f(x)\)の上側の部分
\(y<f(x)\) は 曲線 \(y=f(x)\)の下側の部分
を表すことが分かります。
なお不等号に=がついている場合、例えば \(y≧f(x)\) の場合だと \(y=f(x)\)上の点全体(境界線)も含むことになります。
一般に \(x,y\)についての不等式があるとき、それを満たす点\((x,y)\) 全体の集合をその不等式の表す領域といいます。
さらに不等式 \(f(x,y)>0\) の表す領域を\(f(x,y)\) の正領域、\(f(x,y)<0\) の表す領域を\(f(x,y)\) の負領域といいます。
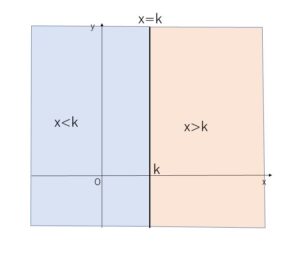
また\(y>f(x)\)の形で表せない、\(x>k\),\(x<k\) の表す領域は、それぞれ\(x=k\) を境界線として右側部分、左側部分となります、
・不等式と領域(円)
次に円に関する不等式の表す領域について考えていきます。
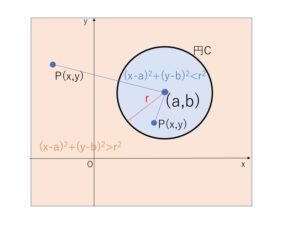
不等式 \((x-a)^2+(y-b)^2<r^2\)・・・(A) (\(r>0\)) について
(A)の両辺は正の値なので平方根をとると
\(\sqrt{(x-a)^2+(y-b)^2}<r\)・・・(B)
これは、\(P(x,y)\)と\((a,b)\)との距離が\(r\)より小さいことを表しています。
距離が\(r\)だと、\((a,b)\)を中心とする半径\(r\)の円\(C\)を表すことになるので、(B)は\(P(x,y)\)が円\(C\)の内部にあることを表すことになります。
同様に \((x-a)^2+(y-b)^2>r^2\) (\(r>0\)) については\(P(x,y)\)が円\(C\)の外部にあることを表しています。
(例題)次の不等式の表す領域を図示せよ。
(1) \(y-2x-4<0\)
(2) \(x>-3\)
(3) \(y≧-x^2-2x+1\)
(4) \(x^2+y^2+2x+4y+1>0\)
(解答)
(1)
\(y-2x-4<0\) を変形すると
\(y<2x+4\)
よって直線 \(y=2x+4\) より下側の部分を表す。
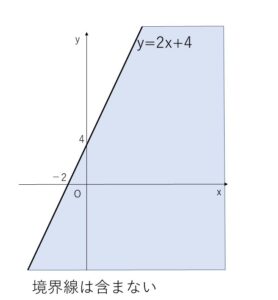
(2)
\(x>-3\) は、\(x=-3\)よりも右側の部分を表す。
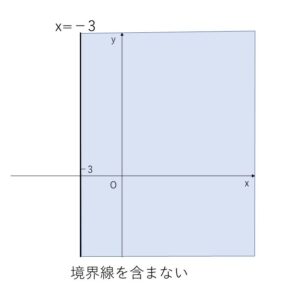
(3)
\(y≧-x^2-2x+1\) の右辺を平方完成して
\(y≧-(x+1)^2+2\) (2次関数のグラフより上側の部分と境界線)
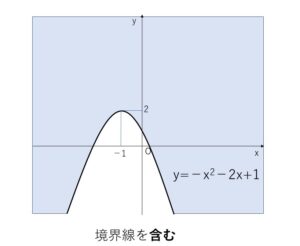
(4)
\(x^2+y^2+2x+4y+1>0\) より
\((x+1)^2+(y+2)^2>4\)
よって中心 \((-1,-2)\),半径\(2\)の円の外側を表す。
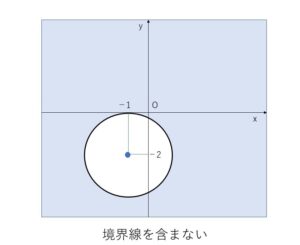
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→連立不等式の表す領域 back→対称移動と曲線の方程式