対称式に関する軌跡・領域に関する問題について見ていきます。
(例題)
(1)座標平面上の点 \((p,q)\) は \(x^2+y^2≦8\) で表される領域を動く。
点\((p+q,pq)\)の動く範囲を図示せよ。
(2)座標平面上の点 \((p,q)\) は \(x^2+y^2≦8\), \(y≧0\) で表される領域を動く。
点\((p+q,pq)\)の動く範囲を図示せよ。
(解答)
(1)
点\((p,q)\)は \(x^2+y^2≦8\) を満たすので
\(p^2+q^2≦8\)
\((p+q)^2-2pq≦8\) だから、\((p+q,pq)\)\(=(X,Y)\) とおくと
\(X^2-2Y≦8\)
よって
\(Y≧\displaystyle\frac{1}{2}X^2-4\)・・・①
\(p+q=X\), \(pq=Y\) のように和と積を別の文字で置き換えたときに、\(X,Y\)が実数であっても、\(p,q\)が実数でないときがあることに気を付けてください。(\((p,q)\)は座標平面上の点なので実数でなくてはならない)
例えば、\(X=p+q=1\), \(Y=pq=2\) のとき、
\(p,q\)は、2次方程式 \(t^2-t+2=0\) の解なのでこれを解くと、\(t=\displaystyle\frac{1±\sqrt{7}i}{2}\) であり、\(p,q\)は実数ではありません。
よって①に加えて、2次方程式の解が実数である条件を加えます。
ここで、\(p,q\)は2次方程式 \(t^2-Xt+Y=0\) の解であり、\(p,q\)が実数であるためには、
\(D=X^2-4Y≧0\) (重解でも\(p=q=\)(実数)となるので適する)
よって \(Y≦\displaystyle\frac{1}{4}X^2\)・・・②
\(X→x\), \(Y→y\)として、①②を図示すると次の通り。
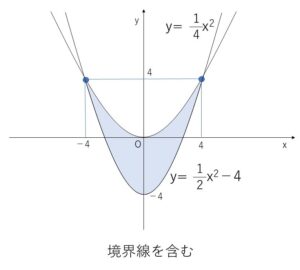
(2)
次に2次方程式 \(t^2-Xt+Y=0\)・・・(A) についてですが、今度は1つの解\(q\)が\(0\)以上です。この問題で出てくる\(p,q\)の式は、\(p^2+q^2\),\(p+q\),\(pq\)ですべて対称式なので、2次方程式(A)が実数解をもち、2解のうち少なくとも1つが\(0\)以上である条件を考えればよいことになります。(2解が例えば \(-1,1\) となれば、対称性から\(p,q\)はどちらでもよいので、\(1\)のほうを\(q\)に割り当てればよい)
\((p+q,pq)\)\(=(X,Y)\) とおく
\(p^2+q^2≦8\)より(1)と同様に \(X^2-2Y≦8\) であるから
\(Y≧\displaystyle\frac{1}{2}X^2-4\)・・・①
ここで、\(p,q\)は2次方程式 \(t^2-Xt+Y=0\)・・・(A) の解。\(p,q\)が実数であり、かつ\(q\)が\(0\)以上である条件を考える。
\(p,q\)の対称性から、2次方程式(A)が実数解をもち、かつ少なくとも1つの解が\(0\)以上であればよいことになる。
(ア)2解とも\(0\)以上 (重解を含む)
(イ)1つが\(0\)以上、もう1つが\(0\)以下
などとしてもよいですが、今回は実数解をもつ場合のうち、2解(重解を含む)がともに負の解になるときを除く方法をとりたいと思います。(補集合の考え方)
(A)が2つの実数解をもつ条件は
\(D=\)\(X^2-4Y≧0\)
つまり、\(Y≦\displaystyle\frac{1}{4}X^2\)・・・②
このうち2解(重解を含む)とも負の解となる条件は、
\(f(t)=t^2-Xt+Y\) とおけば
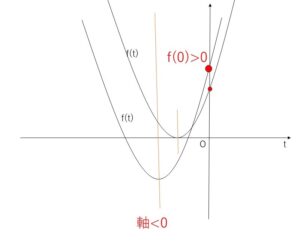
軸<\(0\), \(f(0)>0\)
よって \(\displaystyle\frac{X}{2}<0\) (\(X<0\)), \(Y>0\)・・・③
したがって①②を満たす領域から、③の部分を除いたものが動く範囲となる。
図示すると次の通り。
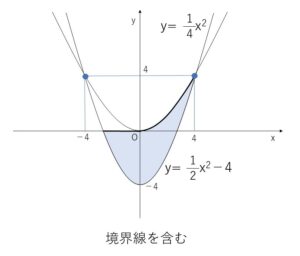
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→ back→通過領域②