一般角

三角関数を学ぶ準備として一般角について見ていきます。

・一般角
図形に現れる角の大きさは、\(0°\)から\(360°\)ですが、例えば歯車の回転運動などを扱う場合には、\(360°\)を超える角度(1回転を超える角度)や、回転の方向(時計回り、反時計回り)も考える必要があります。そこで角の大きさに制限をおかず、向きまで考慮した一般角を導入していきます。

図のように、半直線\(OX\)を固定して、半直線\(OP\)が\(OX\)から出発して点\(O\)を中心として回転したときに\(\angle XOP\)が作られたとします。このとき固定された半直線\(OX\)を始線、動いた方の半直線\(OP\)を動径とよびます。

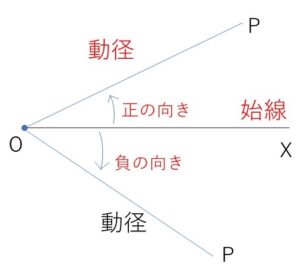
また回転の向きについて、反時計回りの回転の方向を正の向き、時計回りの回転の方向を負の向きとして、正の向きに測った角を正の角、負の向きに測った角を負の角といいます。例えば反時計回りに動径が\(30°\)回転した場合は表す角は\(30°\)、時計回りに\(30°\)回転した場合表す角は\(-30°\)となります。

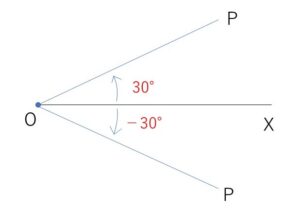
動径\(OP\)の回転を表す角を\(60°\)と指定すると、動径の位置はただ一通りに定まります。一般に角の大きさ\(α\)を指定すると動径の位置は定まり、この動径を角\(α\)の動径といいます。

しかし逆に動径の位置を定めても、\(360°\)回転(\(-360°\)回転)すると元の位置に戻るため、その位置を表す角度は無数にあることになります。
例えば図のように\(\angle XOP=60°\) の位置に動径が位置している場合、表す角としては\(60°\),\(420°(60°+360°)\),\(780°(60°+360°×2)\),\(-300°(60°-360°)\) など、位置を表すある1つの角に\(360°\)の整数倍を加えたものすべてが当てはまることになります。これらの角を動径\(OP\)の表す角と呼びます。

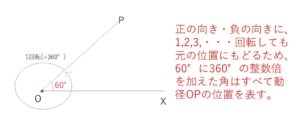
一般に動径\(OP\)の表す角のうちの1つを\(α\)とすると、動径\(OP\)の表す角\(θ\)は

\(θ=α+360°×n\)　 (\(n\)は整数)

となります。

最後に始線や動径を座標平面上で考えていきます。
座標平面上で\(x\)軸の正の部分\(OX\)を始線にとり、動径\(OP\)の表す角を\(θ\)とします。\(OP\)が例えば第1象限にある場合、\(θ\)を第1象限の角とよび、他の象限の場合も同様となります。ただし\(OP\)が座標軸と重なるときはどの象限の角でもないとします。

(例題)
次の角は第何象限の角か。
(1)\(510°\)
(2)\(-510°\)
(3)\(2200°\)

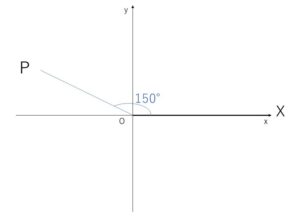
(1)
\(510°=150°+360°×1\)
よって第2象限の角。

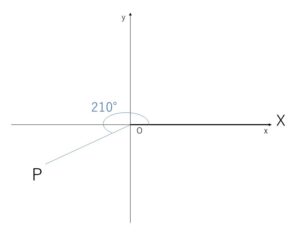
(2)
\(-510°=210°+360°×(-2)\)
よって第3象限の角。

(3)
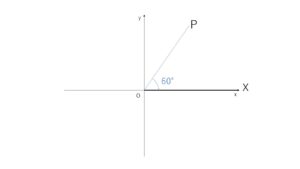
\(2220°=60°+360°×6\)
よって第1象限の角。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→弧度法とその利用