三角関数を利用した図形問題の解法について見ていきます。
(例題)
三角形\(ABC\) の内接円の半径を\(r\)、外接円の半径を\(R\)とする。
また、\(\angle A=2x\), \(\angle B=2y\), \(\angle C=2z\) とする。
(1)辺\(BC\)の長さを、\(r,y,z\) で表せ。
(2)\(r=4R\sin x\sin y\sin z\) であることを示せ。
1つ目は、図形の性質を利用した解法です。こちらは誘導の流れにうまくのっています。
2つ目は、三角形の面積を2パターンで表す方法です。こちらは誘導にあまりのっていないし計算も複雑ですが、式が立式しやすく、式変形のいい練習になると思います。
(解答1)図形的解法
(1)
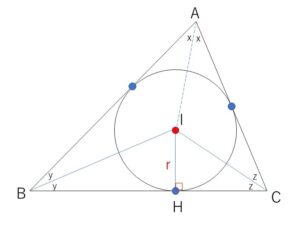
\(△IBC\)内の2つの直角三角形に着目して
\(BH=\displaystyle\frac{r}{\tan y}\), \(HC=\displaystyle\frac{r}{\tan z}\)
よって
\(BC=BH+HC\)
\(=r(\displaystyle\frac{1}{\tan y}+\displaystyle\frac{1}{\tan z})\)
\(=r(\displaystyle\frac{\cos y}{\sin y}+\displaystyle\frac{\cos z}{\sin z})\)
(2)
正弦定理より
\(BC=2R\sin A=2R\sin2x\)
(1)より
\(r(\displaystyle\frac{\cos y}{\sin y}+\displaystyle\frac{\cos z}{\sin z})\)\(=2R\sin2x\)
分母を払うと
\(r(\sin z\cos y+\cos z\sin y)\)\(=2R\sin2x\sin y\sin z\)
\(r\sin(z+y)\)\(=4R\sin x\cos y\sin y\sin z\)・・・①
ここで三角形の内角の和は180°より
\(2x+2y+2z=180°\)
\(y+z=90°-x\)
よって
\(\sin(y+z)\)
\(=\sin(90°-x)\)
\(=\cos x\)
また、\(0°<2x<180°\) より
\(0°<x<90°\) であるから
\(\cos x≠0\)
したがって①の両辺を \(\cos x\) で割って
\(r\)\(=4R\sin x\sin y\sin z\)
(解法2)面積を2通りで表す方法
正弦定理より
\(2R=\displaystyle\frac{BC}{\sin A}=\displaystyle\frac{CA}{\sin B}=\displaystyle\frac{AB}{\sin C}\)
よって三角形の面積\(S\)は
\(S=\displaystyle\frac{1}{2}AB\cdot AC\sin A\)
\(=2R^2\sin A\sin B\sin C\)
また、\(S\)は
\(S=\displaystyle\frac{r}{2}(AB+BC+CA)\)
\(=rR(\sin A+\sin B+\sin C)\)
とも表される。
したがって
\(2R^2\sin A\sin B\sin C\)\(=rR(\sin A+\sin B+\sin C)\)
\(2R\sin A\sin B\sin C\)\(=r(\sin A+\sin B+\sin C)\)・・・(※)
(1)
\(BC=2R\sin A\) と(※)より
\(BC\sin B\sin C\)\(=r(\sin A+\sin B+\sin C)\)
\(0°<B<180°\), \(0°<C<180°\) より、両辺\(\sin B\sin C\) で割り、
\(\sin A=\sin(180°-(B+C))=\sin(B+C)\) だから
\(BC\)
\(=r・\displaystyle\frac{\sin(B+C)+\sin B+\sin C}{\sin B\sin C}\)
\(=r・\displaystyle\frac{\sin B\cos C+\cos B\sin C+\sin B+\sin C}{\sin B\sin C}\)
\(=r・\displaystyle\frac{\sin 2y\cos 2z+\cos 2y\sin 2z+\sin 2y+\sin 2z}{\sin 2y\sin 2z}\)
(分子を \(\sin 2y\) と \(\sin 2z\) でまとめて)
\(=r・\displaystyle\frac{\sin 2y(\cos 2z+1)+\sin 2z(\cos 2y+1)}{\sin 2y\sin 2z}\)
\(=r(\displaystyle\frac{\cos 2z+1}{\sin 2z}+\displaystyle\frac{\cos 2y+1}{\sin 2y})\)
(倍角の公式から)
\(=r(\displaystyle\frac{2\cos^2z}{\sin 2z}+\displaystyle\frac{2\cos^2y}{\sin 2y})\)
\(=r(\displaystyle\frac{2\cos^2z}{2\sin z\cos z}+\displaystyle\frac{2\cos^2y}{2\sin y\cos y})\)
\(=r(\displaystyle\frac{\cos z}{\sin z}+\displaystyle\frac{\cos y}{\sin y})\)
(2)
\(A,B,C\) は三角形の内角なので、いずれも\(0°\)より大きく、\(180°\) より小さい。よって
\(\sin A>0\), \(\sin B>0\), \(\sin C>0\)
(※)より
\(r=\displaystyle\frac{2R\sin A\sin B\sin C}{\sin A+\sin B+\sin C}\)
ここで
\(\sin A+\sin B+\sin C\)
\(=2\sin\displaystyle\frac{A+B}{2} \cos\displaystyle\frac{A-B}{2}+\sin(180°-(A+B))\)
\(=2\sin\displaystyle\frac{A+B}{2} \cos\displaystyle\frac{A-B}{2}+\sin(A+B)\)
\(=2\sin\displaystyle\frac{A+B}{2} \cos\displaystyle\frac{A-B}{2}+2\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A+B}{2}\)
\(=2\sin\displaystyle\frac{A+B}{2}(\cos\displaystyle\frac{A-B}{2}+\cos\displaystyle\frac{A+B}{2})\)
\(=2\sin\displaystyle\frac{A+B}{2}(2\cos\displaystyle\frac{A}{2}\cos\displaystyle\frac{-B}{2})\)
\(=2\sin(90°-\displaystyle\frac{C}{2})(2\cos\displaystyle\frac{A}{2}\cos\displaystyle\frac{B}{2})\)
\(=4\cos\displaystyle\frac{A}{2}\cos\displaystyle\frac{B}{2}\cos\displaystyle\frac{C}{2}\)
\(=4\cos x\cos y\cos z\)
となるから
\(r=\displaystyle\frac{2R\sin A\sin B\sin C}{\sin A+\sin B+\sin C}\)
\(=\displaystyle\frac{2R\sin 2x\sin 2y\sin 2z}{4\cos x\cos y\cos z}\)
\(=\displaystyle\frac{2R\cdot2^3\sin x\cos x\sin y \cos y\sin z \cos z}{4\cos x\cos y\cos z}\)
\(=4R\sin x \sin y \sin z\)
※\(△ABC\) において成り立つ等式
\(\sin A+\sin B+\sin C\)
\(=4\cos\displaystyle\frac{A}{2}\cos\displaystyle\frac{B}{2}\cos\displaystyle\frac{C}{2}\)
が途中で登場しました。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数と領域 back→三角方程式の解の個数