次の問題について考えてみましょう。
\(a,a,a,b,c\) の5個の文字から3個の文字を選んで、1列に並べる方法は何通りあるか。ただし同じ文字は区別しないこととする。
順列や組み合わせの知識があれば、計算で求めることもできますが、一番原始的な方法はすべての場合を書き出してその総数を数えることです。
ただし、起こりうるすべての場合を、もれなく重複なく考えないといけないので、やみくもに書き出すのはよくありません。そこで次の方法をとることでうまく数え上げます。
ただし、起こりうるすべての場合を、もれなく重複なく考えないといけないので、やみくもに書き出すのはよくありません。そこで次の方法をとることでうまく数え上げます。
・辞書式配列
英和辞典の並び方と同じように、順番に文字を並べていきます。
英和辞典の並び方と同じように、順番に文字を並べていきます。
①先頭が\(a\)
2文字目が\(a\) → \(aaa\), \(aab\), \(aac\)
2文字目が\(b\) → \(aba\), \(abc\)
2文字目が\(c\) → \(aca\), \(acb\)
2文字目が\(a\) → \(aaa\), \(aab\), \(aac\)
2文字目が\(b\) → \(aba\), \(abc\)
2文字目が\(c\) → \(aca\), \(acb\)
②先頭が\(b\)
2文字目が\(a\) → \(baa\), \(bac\)
2文字目が\(c\) → \(bca\)
2文字目が\(a\) → \(baa\), \(bac\)
2文字目が\(c\) → \(bca\)
③先頭が\(c\)
2文字目が\(a\) → \(caa\), \(cab\)
2文字目が\(b\) → \(cba\)
2文字目が\(a\) → \(caa\), \(cab\)
2文字目が\(b\) → \(cba\)
並べ方の総数は \(7+3+3=13\)(通り) となります。
・樹形図
枝分かれした図(樹形図)を利用して、各場合を整理します。
枝分かれした図(樹形図)を利用して、各場合を整理します。
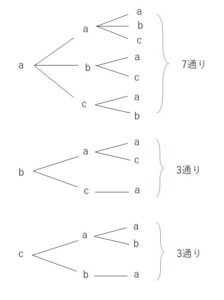
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。