順列には異なる\(n\)個から重複を許してr個を取り出して並べる重複順列というものがありました。組合せにも同様の重複組合せというものがあります。
・重複組合せ
組合わせ\({}_n\mathrm{C}_r\)は、異なる\(n\)個のものから異なる\(r\)個のものを選びましたが、異なる\(n\)個のものから重複を許して\(r\)個をとる組合せ(重複組合せ)の総数について考えていきます。次の例を見てみましょう。
りんご、みかん、バナナの3種類の果物が店頭にたくさんある。
この中から6個の果物を買うとき、何通りの買い方があるか。ただし、1つも買わない果物があってもよいとする。
取り方の順番が ①りんご②りんご③みかん④みかん⑤バナナ⑥バナナ でも
①りんご②りんご③バナナ④バナナ⑤みかん⑥みかん でも買い方としては同じなので、順序は考えません。この例は異なる3個のものから5個取り出す組合せを考えているのですが、同じものを複数選ぶこともありえるので、ただの組合せではなく重複組合せとなっています。
では重複組合せの総数をどうやって求めるのかというと、「 | (しきり)」と「○」を用意して、この並べ方を考えます。
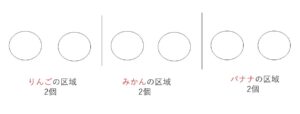
そして、2つのしきりで分かれた3つの区域を、左からりんご、みかん、バナナの区域として、〇の個数はそれぞれの果物の数と考えます。
他にも具体的に例をあげると
〇 | 〇 〇 〇 | 〇 〇 (りんご1個 みかん3個 バナナ2個)
|〇 〇 〇 〇 | 〇 〇 (りんご0個 みかん4個 バナナ2個)
|| 〇 〇 〇 〇 〇 〇 (りんご0個 みかん0個 バナナ6個)
などとなります。
\({}_8\mathrm{C}_6=\displaystyle\frac{8!}{6!2!}=28\)(通り)
\(n-1\)個の「しきり」と、\(r\)個の「〇」を並べる順列を考えて、
\({}_{n}\mathrm{H}_r=\)\({}_{n+r-1}\mathrm{C}_r\)\(=\displaystyle\frac{(n+r-1)!}{r!(n-1)!}\)
となります。
(例題1)
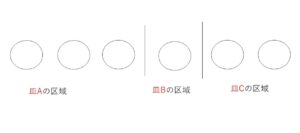
同じ品質の6個のりんごを、3つの異なる皿に盛る方法は何通りあるか。ただしりんごを盛らない皿があってもよいとする。
(解答)
りんご6個を「〇」で表し、仕切り「|」2個と「〇」6個を並べる。仕切り2個で分けられる領域を左から順に皿A,B,Cの領域として、それぞれの領域にある「〇」の個数を各皿に盛られたりんごの数とする。仕切りと〇の並べ方が盛り方の総数になるので、
\({}_8\mathrm{C}_6=\displaystyle\frac{8!}{6!2!}=\)\(28\)(通り)
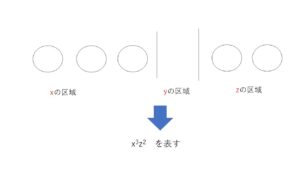
\((x+y+z)^5\)の展開式の異なる項は何個あるか。
掛け合わせる文字1個を「〇」として、〇5個と仕切り「|」2個の並べ方を考える。
仕切りで分けられた領域を左から、\(x,y,z\)の領域として、それぞれの領域にある〇の個数を掛け合わせる文字の個数とする。〇5個と仕切り2個の並べ方の総数が、求める項の個数となるので
\({}_7\mathrm{C}_5=\displaystyle\frac{7!}{5!2!}=\)\(21\)(個)
区別のない3個のさいころをふるとき、目の出方は何通りあるか。
さいころを3つの〇で表し、しきり「|」を5個と一緒に並べる。
仕切りで分けられた6個の領域をそれぞれ1,2,3,4,5,6の目の領域として、領域にある〇の数がその目の出た回数とする。3つの〇と5個のしきりの並べ方の総数が求める場合の数であり、
\({}_8\mathrm{C}_3=\displaystyle\frac{8!}{3!5!}=\)\(56\)(個)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。