次の問題について考えてみましょう。
(例題)
次の条件を満たす整数の組、\((a_1,a_2,a_3,a_4,a_5)\)の個数を求めよ。
(1) \(0<a_1<a_2<a_3\)\(<a_4<a_5<9\)
(2) \(1≦a_1≦a_2≦\)\(a_3≦a_4≦a_5≦4\)
(3) \(0≦a_1<a_2<a_3\), \(a_3>a_4>a_5>0\), \(a_3≦4\)
(解答)
(1)
\(a_1~a_5\)には1から8の数字が当てはまり、どれも異なる値となります。
8個の数字から5個選んで、選んだ数字を小さい順に\(a_1~a_5\)に対応させれば条件を満たす組ができます。
8個の数字から5個選んで、選んだ数字を小さい順に\(a_1~a_5\)に対応させれば条件を満たす組ができます。
1~8の数字から異なる5個の数字を選び、選んだ数字を小さい順に\(a_1~a_5\)に対応させれば条件を満たす組ができる。
よって、求める組の個数は
\({}_8\mathrm{C}_3=\)\(56\)(個)
(2)
\(a_1~a_5\)には1から4の数字が当てはまり、同じものを複数選んでもよいことになります。重複を許して1から4の数字を5個選び、選んだ数字を小さい順に\(a_1~a_5\)に対応させれば条件を満たす組ができます。
また次のように考えてもよいです。
\(a_1~a_5\)を5個の「○」として、領域1,2,3,4に分ける仕切り「|」を3つ用意します。5個の「○」と仕切り「|」を3つを並べ、並べた5個の「〇」を左から順に\(a_1~a_5\)として、それぞれ領域の数字と対応させます。
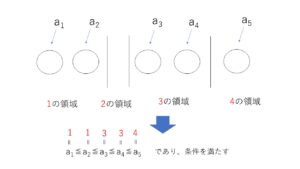
\(a_1~a_5\)を5個の「○」として、領域1,2,3,4に分ける仕切り「|」を3つ用意します。5個の「○」と仕切り「|」を3つを並べ、並べた5個の「〇」を左から順に\(a_1~a_5\)として、それぞれ領域の数字と対応させます。

1~4の数字から重複を許して5個選び、選んだ数字を小さい順に\(a_1~a_5\)に対応させれば条件を満たす組ができる。異なる4個から5個選ぶ重複組合せなので、「○」5個と「|(しきり)」3つを並べる総数を考えて
\({}_8\mathrm{C}_5=\)\(56\)(個)
\({}_8\mathrm{C}_5=\)\(56\)(個)
(3)
2番目の条件、\(a_3>a_4>a_5>0\) から \(a_3\) はどんなに小さくても3であることが分かります。3番目の条件と合わせて、 \(a_3=3,4\) なのでそれぞれについて組の個数を考えます。
\(a_3>a_4>a_5>0\) より、\(a_3≧3\) であり \(a_3≦4\) とあわせて
\(a_3=3,4\)
①\(a_3=3\) のとき
条件は、 \(0≦a_1<a_2<3\), \(3>a_4>a_5>0\) となる。
\(a_1,a_2\)については、数字\(0,1,2\)から異なる2つを選んで小さい順に、\(a_1,a_2\)に対応させればよく、
\(a_4,a_5\)については、数字\(1,2\)から異なる2つを選んで大きい順に、\(a_4,a_5\)とすればよい。よって組の個数は
\({}_3\mathrm{C}_2×{}_2\mathrm{C}_2=3\) (個)
条件は、 \(0≦a_1<a_2<3\), \(3>a_4>a_5>0\) となる。
\(a_1,a_2\)については、数字\(0,1,2\)から異なる2つを選んで小さい順に、\(a_1,a_2\)に対応させればよく、
\(a_4,a_5\)については、数字\(1,2\)から異なる2つを選んで大きい順に、\(a_4,a_5\)とすればよい。よって組の個数は
\({}_3\mathrm{C}_2×{}_2\mathrm{C}_2=3\) (個)
②\(a_3=4\) のとき
条件は、 \(0≦a_1<a_2<4\), \(4>a_4>a_5>0\) となる。
\(a_1,a_2\)については、数字\(0,1,2,3\)から異なる2つを選んで小さい順に、\(a_1,a_2\)に対応させればよく、
\(a_4,a_5\)については、数字\(1,2,3\)から異なる2つを選んで大きい順に、\(a_4,a_5\)とすればよい。
条件は、 \(0≦a_1<a_2<4\), \(4>a_4>a_5>0\) となる。
\(a_1,a_2\)については、数字\(0,1,2,3\)から異なる2つを選んで小さい順に、\(a_1,a_2\)に対応させればよく、
\(a_4,a_5\)については、数字\(1,2,3\)から異なる2つを選んで大きい順に、\(a_4,a_5\)とすればよい。
よって組の個数は
\({}_4\mathrm{C}_2×{}_3\mathrm{C}_2=18\) (個)
\({}_4\mathrm{C}_2×{}_3\mathrm{C}_2=18\) (個)
以上より、求める組の個数は
\(3+18=\)\(21\)(個)
(誤解答)
条件より、
\(0≦a_1<a_2<a_3≦4\), \(4≧a_3>a_4>a_5>0\)
なので、
数字 \(0,1,2,3,4\)から異なる3つを選び、小さい順に\(a_1,a_2,a_3\)とし、その組の個数は \({}_5\mathrm{C}_3=10\) (個)・・・①
数字 \(1,2,3,4\)から異なる3つを選び、大きい順に\(a_3,a_4,a_5\)とし、その組の個数は \({}_4\mathrm{C}_3=4\) (個)・・・②
よって、\(10×4=40\) (個)
※\(a_3\)が2つの不等式にあらわれていて、これは同じ数字でなければいけません。この誤解答では、①で\(a_1=0,a_2=3\)\(,a_3=4\),②で\(a_3=3,\)\(a_4=2\)\(,a_5=1\) なども数えてしまっています。
条件より、
\(0≦a_1<a_2<a_3≦4\), \(4≧a_3>a_4>a_5>0\)
なので、
数字 \(0,1,2,3,4\)から異なる3つを選び、小さい順に\(a_1,a_2,a_3\)とし、その組の個数は \({}_5\mathrm{C}_3=10\) (個)・・・①
数字 \(1,2,3,4\)から異なる3つを選び、大きい順に\(a_3,a_4,a_5\)とし、その組の個数は \({}_4\mathrm{C}_3=4\) (個)・・・②
よって、\(10×4=40\) (個)
※\(a_3\)が2つの不等式にあらわれていて、これは同じ数字でなければいけません。この誤解答では、①で\(a_1=0,a_2=3\)\(,a_3=4\),②で\(a_3=3,\)\(a_4=2\)\(,a_5=1\) なども数えてしまっています。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。