組合せの単元のまとめ問題です。主に組分けがテーマとなっています。
頭の整理に使ってください。
(例題1)
15個の果物を3個の箱に入れたい。次の各場合、それぞれ何通りあるか。ただし、どの箱にも少なくとも1個の果物は入れるものとする。
(1)果物は同種で、箱は異なる。
(2)果物も、箱も同種。
(3)果物も、箱も異なる。
(4)果物は異なるが、箱は同種。
(解答)
(1)
箱をA,B,Cとする。まずすべての箱に1個ずつ果物を入れる。
残り12個の分け方は、異なる3個のものから重複を許して12個を選ぶ組合せを考える。
〇12個と仕切り2個の並び方を考えて、仕切りで区切られた3つの領域を左からA,B,Cの領域として、そこにある〇の数がそれぞれの箱に入る果物の数とする。〇12個と仕切り2個の並び方の総数は、
\({}_{14}\mathrm{C}_{12}=\)\(91\)(通り)
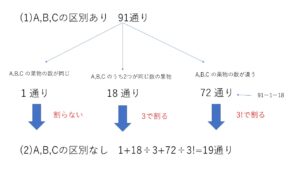
(2)
ただ、(1)の答えをA,B,Cの順列の総数で割ったもの、\(91÷3!\) は答えではありません(そもそも割り切れない)。
(1)を箱の区別をなくしたときに、
①同じものが\(3!\)通りずつあらわれるもの
②同じものが\(3\)通りずつあらわれるもの
③同じものがないもの(区別をなくしても1つかしないもの)
の3パターンがあるからです。
\((A,B,C)=(1,4,10),(1,10,4)\)\(,(4,1,10),(4,10,1)\)\(,(10,1,4),(10,4,1)\)
は(1)では別々のものとして数えていますが、これを区別をなくすと同じになり、同じものが\(3!\)個表れることになります。
②は箱2個の果物の数が同じ場合です。
\((A,B,C)=(3,3,9),(3,9,3)\)\(,(9,3,3)\) は(1)では別々のもので、他に3,3,9個の組合せとなるものはありません。これを区別をなくすと同じものになり、同じものが\(3!÷2!=3\)個表れることになります。
③は箱3個の果物の数が同じ場合です。
\((A,B,C)=(5,5,5)\)は、(1)で1通りで、区別をなくしても1通りです。
(1)で箱の区別をなくす。
[1](1)でA,B,Cの果物の個数が同じ場合は、(5,5,5)個の1通り。
区別をなくしても同じものは表れず1通り。
\(6×3=18\)通り
区別をなくすと同じものが3通りずつ表れる。
[3](1)で3つの箱すべて果物の数が異なる場合は[1][2]と(1)より
\(91-1-6×3=72\) (通り)
区別をなくすと同じものが3!通りずつ表れる。
\(1+18÷3+72÷3!=\)\(19\)(通り)
ただし1個も入らない箱があってはいけないので、
①空き箱が1個 ②空き箱が2個
の場合を除きます。①で例えばA,Bのみに分けるのを \(2^{15}\) 通りと考えると、このなかには②の場合も含まれていることに注意してください。
空き箱あってもよいとすると、全部で\(3^{15}\)通り
このうち空き箱があるのは
①空き箱が1個の場合
例えば、A,Bのみに果物を分けると考えて、片方のみに果物が全部分けられる場合を除いて、\(2^{15}-2\) 通り。
B,Cのみ、A,Cのみも同様だから、全部で \(3(2^{15}-2)\) 通り
②空き箱が2個の場合
Aのみ、Bのみ、Cのみに果物が入る場合で 3通り。
\(3^{15}-3(2^{15}-2)-3=\)\(14250606\) (通り)
(3)で箱の区別をなくすと\(3!\)通りずつ同じものが表れるので
\(14250606÷3!=\)\(2375101\) (通り)
(例題2)
白球5個、赤球3個、黒球2個がある。次のような方法は何通りあるか。
(1)10個の球から6個を取り出す方法。ただし1個も取り出さない種類があってもよい。
(2)10個の球を6人に分ける方法。ただし1個ももらわない人があってもよい。
(2)10個の球を2組に分ける方法。
(解答)
(1)
具体的に個数を書き出すと、
(白、赤、黒)=(5,1,0),(5,0,1),(4,2,0),(4,1,1),(4,0,2),(3,3,0),(3,2,1),(3,1,2),(2,3,1),(2,2,2),(1,3,2)
の 11通り
(2)
②次に赤球3個を6人に分ける。
③最後に黒球2個を6人に分ける。
と3段階で考えます。
\({}_{10}\mathrm{C}_5\) 通り。
同様に、赤球3個、黒球2個を6人に分けると、求める場合の数は
\({}_{10}\mathrm{C}_5×{}_8\mathrm{C}_3×{}_7\mathrm{C}_2\)
\(=252×56×21\)
\(=\)\(296352\) (通り)
1個も分けられない組があってもよいとすると、(2)と同様に重複組合せを考えて
\({}_{6}\mathrm{C}_5×{}_4\mathrm{C}_3×{}_3\mathrm{C}_2\)
\(=6×4×3=72\) (通り)
\(70÷2!=\)\(35\) (通り)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。