次の組分けの問題について考えてみます。今回も区別できるもの、できないものに気を付けます。
(例題)
6枚のカード、1,2,3,4,5,6がある。
(1)6枚のカードを組Aと組Bに分ける方法は何通りあるか。ただし、各組に少なくとも1枚は入るものとする。
(2)6枚のカードを2組に分ける方法は何通りあるか。
(3)6枚のカードを同じ大きさの3個の箱に分けるとき、カード1,2を別々の箱に入れる方法は何通りあるか。ただし、空の箱はないものとする。
6枚のカードは異なるものなので区別できるものです。
分けるグループ(組と箱)の区別の可否については(1)~(3)それぞれで考えます。
前回との違いは、今回の問題では組や箱に分ける枚数が決まっていないことです。
分けるグループ(組と箱)の区別の可否については(1)~(3)それぞれで考えます。
前回との違いは、今回の問題では組や箱に分ける枚数が決まっていないことです。
(解答)
(1)
組A,Bと書かれているので区別できるものです。
6枚のカードそれぞれA,Bの2通りの分け方があるので、\(2^6\)を計算します。(\(6^2\)ではありません)
あとは片方に全部カードが分けられる場合を除きます。
6枚のカードそれぞれA,Bの2通りの分け方があるので、\(2^6\)を計算します。(\(6^2\)ではありません)
あとは片方に全部カードが分けられる場合を除きます。
6枚のカードを、それぞれA,Bの2通りに分ける方法は
\(2^6\) (通り)
このなかで、6枚すべてがAまたはBに分けられる方法は
\(2\) (通り)
よって、求める場合の数は
\(2^6-2=\)\(62\)(通り)
\(2^6\) (通り)
このなかで、6枚すべてがAまたはBに分けられる方法は
\(2\) (通り)
よって、求める場合の数は
\(2^6-2=\)\(62\)(通り)
(2)
ただの2組なので区別できないものです。(1)で区別をなくした場合を考えましょう。
(1)でA,Bの区別をなくすと、同じものが\(2!\)ずつ出てくるので
\(62÷2!=\)\(31\)(通り)
\(62÷2!=\)\(31\)(通り)
例えば、A{1,2,3,4}, B{5,6} と A{5,6} B{1,2,3,4} は(1)では区別できるものでしたが、(2)では同じものとなります。
(3)
同じ大きさの箱なので区別ができないものです。
ただし、カード1と2を別々の箱に入れるという条件があるので、
①カード1が入っている箱 ②カード2が入っている箱 ③カード1,2のどちらも入っていない箱
と3箱に特徴があるので、区別できるものになります。
ただし、カード1と2を別々の箱に入れるという条件があるので、
①カード1が入っている箱 ②カード2が入っている箱 ③カード1,2のどちらも入っていない箱
と3箱に特徴があるので、区別できるものになります。
たとえば、次の分け方だとそれぞれは区別できるものになっています。
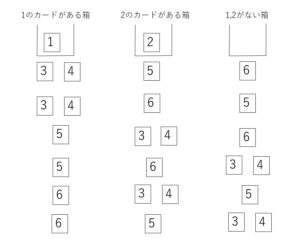
1,2のカードをなくした場合には、区別できないものになりますね。
カード1が入る箱を①、カード2が入る箱を②、どちらも入らない箱を③とする。
残りのカード3,4,5,6を、①~③のどれかに分ける方法は \(3^4\) (通り)
③に1枚もカードが入らない方法は、A,Bのみにカード3,4,5,6を入れる方法なので \(2^4\) (通り)
よって \(3^4-2^4=81-16=\)\(65\)(通り)
次回以降も、区別できる・できないが重要になってきます。注意しましょう。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。