次の問題について考えてみましょう。
(例題)
\(a\)3個、\(b\)2個、\(c\)2個の計7個の文字を1列に並べる方法は何通りあるか。
同じもの(区別ができない)が何個か含まれている順列です。
この問題のアプローチの仕方として2つのパターンがあります。
(解法1)同じものを入れる位置を決める方法
全部で7文字を並べるので、7個の位置に文字を入れると考えます。
(1)まず7個の位置から3個の\(a\)を入れる位置を決めるので、この方法は \({}_7\mathrm{C}_3\) 通り
(2)次に残り4個の位置から2個の\(b\)を入れる位置を決めるので、この方法は \({}_4\mathrm{C}_2\) 通り
(3)残った2個の位置から2個の\(c\)を入れる位置を決めるので、この方法は \({}_2\mathrm{C}_2\) 通り
以上(1)~(3)より
\({}_7\mathrm{C}_3×{}_4\mathrm{C}_2×{}_2\mathrm{C}_2=\)\(210\)(通り)
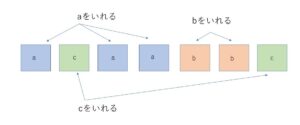
(解法2)同じものをまず区別して考えて、あとで区別をなくす方法
3つの\(a\),2つの\(b\)、1つの\(c\)を区別あるものとして、
\(a_1,a_2,a_3\) \(b_1,b_2\) \(c_1,c_2\) とする。
この区別された7個の文字の順列の総数は \(7!\) 通り。
(1)\(a_1=a_2=a_3=a\) として区別をなくすと 同じものが\(3!\)ずつ出てくる。
(2)次に、\(b_1=b_2=b\) として区別をなくすと 同じものが\(2!\)ずつ出てくる。
(3)さらに、\(c_1=c_2=c\) として区別をなくすと 同じものが \(2!\)ずつ出てくる。
(1)~(3)より、求める場合の数は
\(\displaystyle\frac{7!}{3!\cdot2!\cdot2!}=\)\(210\)(通り)・・・(A)
※(解法1)の式を変形すると
\({}_7\mathrm{C}_3×{}_4\mathrm{C}_2×{}_2\mathrm{C}_2\)
\(=\displaystyle\frac{7\cdot6\cdot5}{3!}×\displaystyle\frac{4\cdot3}{2!}×\)\(\displaystyle\frac{2\cdot1}{2!}\)\(=\displaystyle\frac{7!}{3!\cdot2!\cdot2!}\)
と(A)式と同じになります。
同様に考えると、一般に、\(n\)個のもののうち、\(p\)個は同じもの、\(q\)個は他の同じもの、\(r\)個はまた他の同じもの・・・であるとき、\(n\)個のもの全部を並べて作った順列の総数は
\({}_n\mathrm{C}_p×{}_{n-p}\mathrm{C}_q\)\(×{}_{n-p-q}\mathrm{C}_r×・・・\)
つまり
\(\displaystyle\frac{n!}{p!q!r!・・・}\) (\(p+q+r+\)\(・・・=n\))
となります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。