文字の順序が指定された、順列の個数の数え上げについて考えていきます。
(例題)
medicineのすべての文字を用いてつくる順列のうち
(1)異なる順列の数を求めよ。
(2)子音 m,d,c,n がこの順に並ぶものの数を求めよ。
(解答)
(1)
(1)は同じものを含む順列です。
8文字はそれぞれ、m,d,c,n,e,e,i,i だから
\(\displaystyle\frac{8!}{2!2!}=\)\(10080\)(通り)
\(\displaystyle\frac{8!}{2!2!}=\)\(10080\)(通り)
(2)
「m,d,c,n がこの順に並ぶ」は隣り合って(連続して)いなくてもよく、間に何か挟まっていてもよいと捉えてください。もしくっついて並ぶ場合を聞いている場合には、「隣り合って並ぶ」や「mdcnという並び」などといった表現になります。
このタイプの問題では次のように考えます。
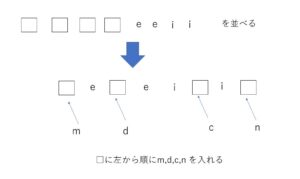
m,d,c,nの入る枠を□が4つある(区別できない枠)と考えて、□4つとe,e,i,iを並べます。あとは□の左から順番にm,d,c,nを入れていけば条件に合う順列になります。
m,d,c,nの入る枠を□が4つある(区別できない枠)と考えて、□4つとe,e,i,iを並べます。あとは□の左から順番にm,d,c,nを入れていけば条件に合う順列になります。

4個の区別できない□、2個のe、2個のi を並べて、□に左から順に、m,d,c,nを入れれば条件に合う順列となる。よってその総数は
\(\displaystyle\frac{8!}{4!2!2!}=\)\(420\)(通り)
\(\displaystyle\frac{8!}{4!2!2!}=\)\(420\)(通り)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。