網目上の道路の最短経路の数を数え上げるには、同じものを含む順列の考え方を利用します。
(例)
次のような街路にそって、AからBまで行く方法は何通りあるか。ただし最短経路を通るものとする。
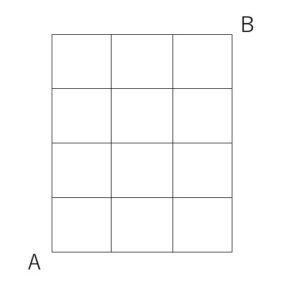
最短経路なので、左に進んだり下に進んだりはできません。よって右と上の移動だけになりますが、右と上だけの進行でBにたどり着くには、合計「右3回、上4回」の移動となります。「右3回、上4回」の「右」と「上」の移動はどの順番で移動してもよいので、街路の右方向と上方向の移動を「右」と「上」の文字で表すことによって、「右右右上上上上」を7文字と考えて、同じものを含む順列を考えることでその経路の総数を求めることができます。例えばその1つである「右上右上右上上」は次の経路と対応していて、他の順列と経路についても、1:1に対応しています。
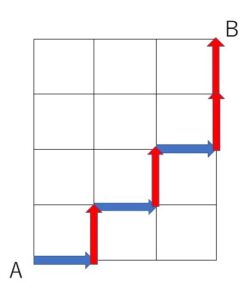
経路の個数は、\(\displaystyle\frac{7!}{3!4!}=\)\(35\)(通り) です。
(\({}_7\mathrm{C}_3\)でもよいです)
これを踏まえて次の例題を見ていきます。
(例題1)
次の図のように、道路が碁盤の目のようになった街がある。地点Aから地点Bまでの長さが最短の道を行くとき、次の場合には何通りの道順があるか。
(1)全部の道順
(2)地点Cを通る
(3)地点Pを通らない
(4)地点Pと地点Qのどちらも通らない
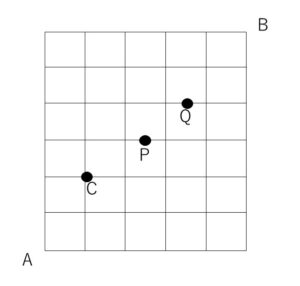
(解答)
(1)
右方向の進行を右、上方向の進行を上とすると、道順は右5個,上6個の順列で表されるので、
\(\displaystyle\frac{11!}{5!6!}=\)\(462\)(通り)
(2)
\(\displaystyle\frac{3!}{1!2!}=3\)(通り)
CからBまでの道順は、右4個,上4個の順列を考えて、
\(\displaystyle\frac{8!}{4!4!}=70\)(通り)
よって、\(3×70=\)\(210\)(通り)
\(\displaystyle\frac{5!}{2!3!}×\displaystyle\frac{5!}{2!3!}=\)\(100\)(通り)
よって、Pをとらない道順は(1)より
注意してほしいのですが、「PまたはQを通る道順」の個数は単純に (Pを通る道順の個数)+(Qを通る道順の個数)ではありません。(Pを通る道順の個数)の中にはPとQのどちらも通るものが含まれ、同じく(Qを通る道順の個数)の中にはPとQのどちらも通るものが含まれるため、余分に1回数えられている個数を(PもQのどちらも通る道順の個数を) 1回除いてあげないといけません。
PまたはQを通る道順を考える。
Pを通る道順は(3)より \(100\)(通り)
Qを通る道順は、
\(\displaystyle\frac{7!}{3!4!}×\displaystyle\frac{3!}{1!2!}\)\(=105\) (通り)
PとQのどちらも通る道順は、
\(\displaystyle\frac{5!}{2!3!}×\displaystyle\frac{3!}{1!2!}\)\(=30\) (通り)
よって、PまたはQを通る道順は、
\(100+105-30=175\)(通り)
\(462-175=\)\(287\)(通り)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。