平面図形の塗り分けと組合せ

平面図形の塗り分けの問題について考えていきます。
ポイントは固定する色の選び方です。

(問題)
2×2の正方形のマス目をA,B,C,Dの4色から何色かを用いて塗り分ける方法は何通りあるか。ただし、全部1色でもよく、平面内で回転させると同じになる塗り方は同じ塗り方と考える。

4色、3色、2色、1色で場合分けします。
回転させると一致するものは同じなので、円順列を考えます。

(解答)

①4色を使う場合
円順列を考えて、\((4-1)!=6\) (通り)

②3色を使う場合

まず4色から3色を選び(\({}_4\mathrm{C}_3\))、3色のうち2回使う色を1色選びます(\({}_3\mathrm{C}_1\))。
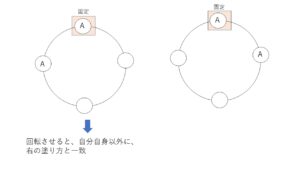
例えばAABCで塗るとき、具体的に数えてももちろんよいですが、計算で求めてみます。このとき、1つを固定する方法で考えると、固定する色は2色使うAを選ぶより、1色しか使わない色BCを選んだ方がよいです。2色使うAを固定すると、例えば次のような2パターンは回転させると自分自身以外にも、重なる相手があるから計算で求めるとすると重複分を考えないといけません。(B or Cで固定すると回転させると自分自身にしか重ならない)

4色から使用する3色を選び、3色から2回使う色を1色選ぶ方法は、
\({}_4\mathrm{C}_3×{}_3\mathrm{C}_1\) (通り)

例えば、AABCと選ぶとき、Cを円順列の一番上に固定すると、残りAABの順列の総数は、\(\displaystyle\frac{3!}{2!1!}\)\(=3\) (通り)

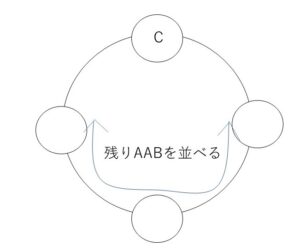
平面　塗分け　C固定

よって、3色を用いたときの場合の数は
\({}_4\mathrm{C}_3×{}_3\mathrm{C}_1×3\)\(=36\)(通り)

③2色を使う場合

4色から2色を選びます(\({}_4\mathrm{C}_2\))。
選んだ2色が例えばAとBだと、Aの使う回数に着目して
①ABBB ②AABB ③AAAB　の塗り方があります。②についは一番使用しない色でも2回使っているので、計算で求めると面倒です。なので、大した数にならないので①～③まとめて具体的に書き上げて数えます。

4色から2色選ぶ方法は、\({}_4\mathrm{C}_2=6\) (通り)

選んだ2色がABのとき、塗り方は次の4通りとなる。

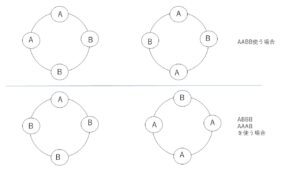
よって2色を用いた場合の数は
\(6×4=24\) (通り)

④1色を使う場合
4色から1色を選び、例えばAを選んだときは、全部Aで塗るので塗り方は1通り。
よって、\({}_4\mathrm{C}_1=4\) (通り)

以上①～④より
\(6+36+24+4=\)\(70\)(通り)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→立方体の塗り分け　 back→最短経路