微分には様々な用途がありますが、そのうちの1つを簡単に言ってしまうと「グラフを書くための道具」です。今までグラフを書くときには具体的な点をいくつか座標平面に書いて線で結ぶという作業をしましたが、この微分のとっかかりも似たようなものです。
・平均変化率
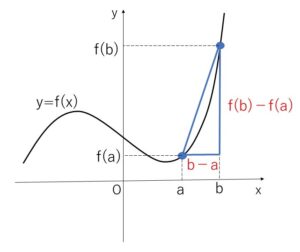
関数 \(y=f(x)\) において、\(x\)の値が\(a\)から\(b\)まで変化するとき、\(y\)の値は\(f(a)\)から\(f(b)\)まで変化します。このとき\(x\)の変化量に対する\(y\)の変化量の割合
\(\displaystyle\frac{f(b)-f(a)}{b-a}\)
を、\(x\)が\(a\)から\(b\)まで変化するときの、関数\(y=f(x)\) の平均変化率といいます。
図を見てもらえれば分かると思いますが、この平均変化率は2点を結ぶ直線の傾きとなります。
そこで2点間の間がどうなっているかを考えていくわけですがその方法は単純で、2点を近づけてその間を狭くしてやればいいだけです。ただし2点を近づけるといってもただ近づけるというわけではなく、ほとんど重なるくらいに近づけていきます。これが極限を考えるということであり、以下詳しく説明していきます。
・極限値
関数 \(f(x)=x^2\) において、2点 \((1,1)\), \((1+h,(1+h)^2)\) の平均変化率を考えると
\(\displaystyle\frac{(1+h)^2-1}{(1+h)-1}=\displaystyle\frac{h^2+2h}{h}\)・・・①
であり、\(h\)の値を
\(0.1,0.01,0.001,0.0001,0.00001,\cdots\)
と\(0\)に近づけていきます。(このとき2点は近づいていくことになる)
すると、平均変化率の値は①より
\(2.1,2.01,2.001,2.0001,2.00001,\cdots\)
と一定の値\(2\)に限りなく近づいていくことになります。
今、\(h\)を正の値の方から\(0\)に近づけましたが、負の値の方向から近づけても同様に\(2\)に近づくことになります。
平均変化率 \(\displaystyle\frac{h^2+2h}{h}\) は \(h=0\) では定まりませんが、\(h\)が\(0\)とは異なる値をとりながら\(0\)に限りなく近づくとき、\(\displaystyle\frac{h^2+2h}{h}\) は一定の値\(2\)に限りなく近づくことになり、この値\(2\)を、\(h\)が限りなく近づくときの\(\displaystyle\frac{h^2+2h}{h}\) の極限値といい、次のように表します。
\(\displaystyle\lim_{h \to 0}\displaystyle\frac{h^2+2h}{h}=2\)
\(\displaystyle\lim_{h \to 0}\displaystyle\frac{h^2+2h}{h}=\displaystyle\lim_{h \to 0}(h+2)=2\)
\(h\)で割ることができるのは、\(h\)が\(0\)とは異なる値だからです(ただし限りなく\(0\)には近いです)。それと\(0\)とは違う値なのに、最後に\(h=0\)を代入していてよいのかということですが、\(h\)を\(0\)に近づければ\(h+2\)は\(2\)に近づくということで納得してください。
また、一般的には \(y=f(x)\) において \(x\)が\(a\)と異なる値をとりながら限りなく\(a\)に近づくとき、\(f(x)\)が一定の値\(α\)に限りなく近づくならば
\(\displaystyle\lim_{x \to a}f(x)=α\)
または
\(x \to a\) のとき \(f(x) \to α\)
と表し、\(α\)を\(x\)が\(a\)に近づくときの\(f(x)\)の極限値といいます。
・微分係数
そして関数 \(y=f(x)\)における 平均変化率の極限を考えていきます。
関数 \(y=f(x)\) の \(a\)から\(b\)まで変化するときの平均変化率
\(\displaystyle\frac{f(b)-f(a)}{b-a}\)
において、\(b\)を限りになく\(a\)に近づけたとき、この平均変化率がある一定の値に限りなく近づくならば、その極限値を、関数 \(y=f(x)\) の \(x=a\) における微分係数といい、\(f'(a)\) で表します。つまり
\(f'(a)=\displaystyle\lim_{b \to a}\displaystyle\frac{f(b)-f(a)}{b-a}\)
であり、\(b-a=h\) と置き換えると、\(b \to a\) のとき \(h \to 0\) だから
\(f'(a)=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(a+h)-f(a)}{h}\)
となります。
最後にこの微分係数\(f'(a)\) が \(y=f(x)\) のグラフにおいてどのような意味をもつかを考えていきます。
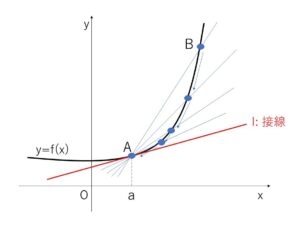
グラフ上に\(x\)座標がそれぞれ \(a\), \(a+h\) である2点\(A,B\)をとると、
\(\displaystyle\frac{f(a+h)-f(a)}{h}\)
は直線\(AB\)の傾きを表していることは先ほどやりました。
ここで、\(h\)を\(0\)に限りなく近づけると、点\(B\)はグラフ上を動いて限りなく点\(A\)に近づくことになります。このとき
\(f'(a)=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(a+h)-f(a)}{h}\)
だから、直線\(AB\)は点\(A\)を通る傾き\(f'(a)\)の直線\(l\)に限りなく近づくことになります。
この直線\(l\)を点\(A\)における曲線\(y=f(x)\)の接線、点\(A\)を接点とよびます。
またこのとき、「直線\(l\)は\(y=f(x)\)と点\(A\)で接する」と表現します。
曲線上に異なる2点\(A,B\)があり、\(B\)が\(A\)に限りなく近づくとき、直線\(AB\)が限りなく直線\(l\)に近づくとする。この直線\(l\)を点\(A\)における接線という。また、接線の傾きは \(f'(a)\) になる。
(似たような名前の「点\(A\)を通る接線」というものもありますが、「点\(A\)における接線」と、「点\(A\)を通る接線」は違うものです。点\(A\)における接線は接点が\(A\)である必要があります。一方点\(A\)を通る接線は点\(A\)を通りさえすればよいので、他の点における接線がたまたま点\(A\)を通る場合でも、点\(A\)における接線でもどちらも構いません。)
一般に整式で表される関数 \(y=f(x)\)と、 点\(A(a,f(a))\)を通る直線\(l\) \(y=g(x)\)について
「\(f(x)-g(x)=0\) が \(x=a\) を重解にもつ \(⇔\) 直線\(l\) が点\(A\)で接する」
ということが成り立ちます。証明は簡単ですが積の微分(数Ⅲ)の知識が必要なので別の機会にして、今回は例題で具体的な例で確かめてみます。
(例題)
関数 \(y=3x^2-5x\) について、次のものを求めよ。
(1) \(x=2\) から \(x=4\) まで変化するときの平均変化率
(2) \(x=2\) における微分係数
(3) \(x=2\) における接線の傾き
(解答)
\(f(x)=3x^2-5x\) とおく。
(1)
(平均変化率)
\(=\displaystyle\frac{f(4)-f(2)}{4-2}\)
\(=\displaystyle\frac{28-2}{2}\)
\(=13\)
(2)
\(f'(2)\)
\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(2+h)-f(2)}{h}\)
\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{\{3(2+h)^2-5(2+h)\}-2}{h}\)
\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{3h^2+7h}{h}\)
\(=\displaystyle\lim_{h \to 0}(3h+7)\)
\(=7\)
(3)
\(x=2\)における接線の傾き\(m\)は、\(f'(2)\)だから(2)より
\(m=f'(2)\)\(=7\)
※接線を求めると、\((2,f(2))\) を通るから
\(y-f(2)=f'(2)(x-2)\)
\(y-2=7(x-2)\)
よって接線の方程式は
\(y=7x-12\)・・・(ア)
\(y=3x^2-5x\) と (ア)を連立して整理すると
\(x^2-4x+4=0\)
\((x-2)^2=0\)
となり、\(x=2\) が重解となっています。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極限値