今回は2曲線が共通接線をもつ場合で、それぞれ異なる点で接している問題について見ていきます。
①一方の曲線の接線がもう一方に接する
or
②2つの曲線の接線が一致する
特に整式の場合には①で重解をもつ条件に置き換えることができます。
②では、接点の\(x\)座標をそれぞれ、\(s,t\) とおくことになり2文字になり式が複雑になるので、整式の場合には①で解いたほうが楽になることが多いです。
なお、これら①②どちらも2曲線が接する(共有点で接する)場合を含みますが、一般的には接点が同じであるとは限りません。
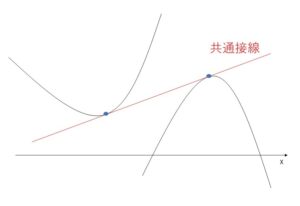
(例題1)
\(a\)を定数とする。2つの放物線
\(C_1:y=-x^2\)
\(C_2:y=3(x-1)^2+a\)
について、\(C_1,C_2\)の両方に接する直線が2本存在するための\(a\)の条件を求めよ。
\(C_1\)のほうが式が簡単なので、こちらの接点を \((t,-t^2)\) とおきます。
(解答)
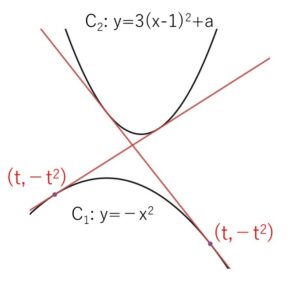
\(C_1\) 上の点を \((t,-t^2)\) とおくと、\(y’=-2x\) より接線の方程式は
\(y=-2t(x-t)-t^2\)
だから
\(y=-2tx+t^2\)・・・①
①と\(C_2\)より \(y\)を消去すると
\(-2tx+t^2=3(x-1)^2+a\)
\(x\)について整理して
\(3x^2+2(t-3)x-t^2+a+3=0\)・・・②
\(C_2\)と①は接するので\(x\)の方程式②は重解をもつから
\(\displaystyle\frac{D}{4}=0\)
\((t-3)^2-3(-t^2+a+3)=0\)
\(t\)について整理して
\(4t^2-6t-3a=0\)・・・③
2次関数では接点が異なれば接線も異なるので(下記参照)、異なる2つの実数解をもてば異なる2つの接線が存在することになります。
2次関数では接点が異なれば接線も異なることに注意すると、
\(t\)の方程式③が異なる実数解をもてば、\(C_1\)上で異なる2つの接点をもち、接線が2つ存在することになる。
よって③について
\(\displaystyle\frac{D}{4}>0\)
\(9+12a>0\)
\(a>-\displaystyle\frac{3}{4}\)
(注)
「2次関数では接点が異なれば接線も異なる」ことはグラフを考えても明らかですが、丁寧にやるなら
\(y=px^2+qx+r\) (\(p≠0\))
において
\(y’=2px+q\)
だから、導関数は1次関数で\(x\)が異なれば、\(y’\)つまり接線の傾きが異なることになる。
したがって、接点が異なれば接線も異なることになります。
※ちなみに接線が一致する方針で解くと
\(C_1\) の接点を \((t,-t^2)\)
\(C_2\) の接点を \((s,3(s-1)^2+a)\)
とおくと、\(C_2\)については
\(y’=6(x-1)\)
となるので接線はそれぞれ
\(y=-2t(x-t)-t^2\)
\(y=6(s-1)(x-s)+3(s-1)^2+a\)
整理して
\(y=-2tx+t^2\)
\(y=6(s-1)x-3s^2+3+a\)
係数を比較すると
\(-2t=6(s-1)\)・・・(1)
\(t^2=-3s^2+3+a\)・・・(2)
(1)から
\(s=-\displaystyle\frac{1}{3}t+1\)
(2)に代入して\(s\)を消去すると
\(4t^2-6t-3a=0\)・・・③
と先ほどの解答と同じ式が得られます。
(\(t\)が実数ならば、(1)より\(s\)も実数としてとれる)
(例題2)
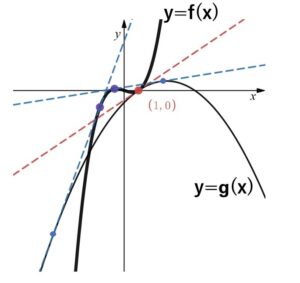
ある直線が1点\((1,0)\)で2曲線
\(y=f(x)=x^3-x\)
\(y=g(x)=-\displaystyle\frac{1}{2}x^2+ax+b\)
に同時に接しているという。このとき、\(a=\)( ), \(b=\)( ) である。またこの直線のほかに、この2曲線のいずれにも接する直線は2本あって、それらと \(y=f(x)\) との接点の\(x\)座標をすべて挙げると( )である。
(前半部分)
\(f'(x)=3x^2-1\)
\(g'(x)=-x+a\)
2曲線が\((1,0)\)で接しているので
\(f(1)=g(1)\)
\(f'(1)=g'(1)\)
\(0=-\displaystyle\frac{1}{2}+a+b\)・・・①
\(2=-1+a\)・・・②
①②より
\(a=3\), \(b=-\displaystyle\frac{5}{2}\)
(後半部分)
\(g(x)=-\displaystyle\frac{1}{2}x^2+3x-\displaystyle\frac{5}{2}\)
であり、\(g(x)\)のほうが2次関数なので、\(f(x)\)のほうの接点を\((t,f(t))\)とおいて接線を求めて、\(g(x)\)と接する条件(重解をもつ条件)を考えます。
\(f(x)=y=x^3-x\) 上の点を \((t,t^3-t)\) とおくと、この点における接線は
\(y=(3t^2-1)(x-t)+t^3-t\)
整理して
\(y=(3t^2-1)x-2t^3\)・・・③
③と \(y=g(x)\) より
\((3t^2-1)x-2t^3=-\displaystyle\frac{1}{2}x^2+3x-\displaystyle\frac{5}{2}\)
\(x\)について整理すると
\(x^2+2(3t^2-4)x-4t^3+5=0\)・・・④
\(x\)の方程式④は重解をもつので
\((3t^2-4)^2-(-4t^3+5)=0\)・・・⑤
⑤を整理すると
\(9t^4+4t^3-24t^2+11=0\)
\((t-1)^2(9t^2+22t+11)=0\)
\(t=1\) は、2曲線が\((1,0)\)で同時に接している場合だから
\(9t^2+22t+11=0\) を解いて
\(t=\displaystyle\frac{-11±\sqrt{22}}{9}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2重接線 back→共通接線①(2曲線が接する)