法線

法線の方程式について学んでていきます。

・法線

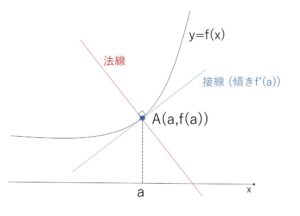
曲線 \(y=f(x)\) 上の点\(A(a,f(a))\) を通り、点\(A\)における接線と直交する直線を、点\(A\)における法線(ほうせん)とよびます。

点\(A\)における接線の傾きは、\(f'(a)\) なので、
\(f'(a)≠0\) のとき、直交するときは傾きの積が\(-1\)だから、法線の傾きは \(-\displaystyle\frac{1}{f'(a)}\)

したがって、点\(A\)における法線の方程式は

\(y-f(a)=-\displaystyle\frac{1}{f'(a)}(x-a)\)  (\(f'(a)≠0\))

(例題1)
(1) \(y=x^2\) 上の 点\(P(t,t^2)\) における法線の方程式を求めよ。

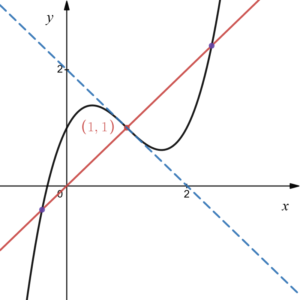
(2) 曲線 \(y=x^3-3x^2+2x+1\) について、傾きが\(1\)である法線の方程式と、この法線と曲線との共有点の座標を求めよ。

(解答)
(1)

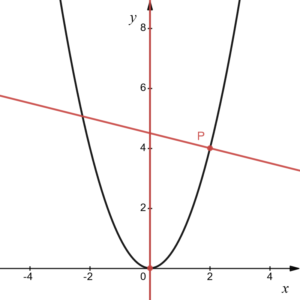
\(y’=2x\) より
\(t≠0\) のとき法線の方程式は
\(y-t^2=-\displaystyle\frac{1}{2t}(x-t)\)

両辺\(2t\)倍して整理すると
\(x+2ty-2t^3-t=0\)・・・①

\(t=0\) のとき法線の方程式は
\(x=0\) (\(y\)軸)であり、これは①で\(t=0\) とすればよい。

したがって法線の方程式は
\(x+2ty-2t^3-t=0\)

(2)
\(y=x^3-3x^2+2x+1\)・・・② において
\(y’=3x^2-6x+2\)

法線の傾きが\(1\)だから
\(-\displaystyle\frac{1}{3x^2-6x+2}=1\)
\(3x^2-6x+2=-1\)
(\(3x^2-6x+2≠0\)を満たす)
\(3(x^2-2x+1)=0\)
\((x-1)^2=0\)
\(x=1\)

\(x=1\) のとき \(y=1-3+2+1=1\) より
法線の方程式は
\(y-1=1\cdot(x-1)\)
\(y=x\)

また \(y=x\) と ②より \(y\)を消去して
\(x^3-3x^2+2x+1=x\)
\(x^3-3x^2+x+1=0\)・・・③

\((x-1)(x^2-2x-1)=0\)

\(x=1,1±\sqrt{2}\)

\(y=x\) より共有点の座標は
\((1,1),(1+\sqrt{2},1+\sqrt{2}),(1-\sqrt{2},1-\sqrt{2})\)

(例題2)
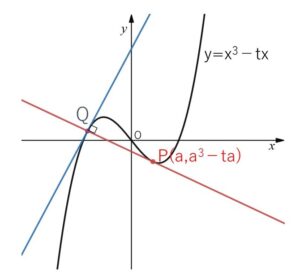
曲線 \(C:y=x^3-tx\) 上の点\(P(a,a^3-ta)\)  (\(a>0\)) における接線が\(C\)と交わる点を\(Q\)とする。

(1)点\(Q\)の\(x\)座標を\(a\)を用いて表せ。
(2)点\(Q\)における\(C\)の接線が直線\(PQ\)と直交するための条件を求めよ。
(3) (2)を満たす \(a>0\) の値がただ1つ決まるのは\(t\)がどのような値のときか。

(解答)
(1)

\(y=x^3-tx\)・・・①　において
\(y’=3x^2-t\)

よって、点\(P(a,a^3-ta)\) における接線の方程式は
\(y=(3a^2-t)(x-a)+(a^3-ta)\)
整理すると
\(y=(3a^2-t)x-2a^3\)・・・②

①②より
\(x^3-tx=(3a^2-t)x-2a^3\)
\(x^3-3a^2x+2a^3=0\)

\((x-a)^2(x+2a)=0\)

したがって 点\(Q\)の\(x\)座標は
\(x=-2a\)

(2)

点\(Q\)の\(y\)座標は
\(y=(-2a)^3-t(-2a)=-8a^3+2ta\)

よって、直線\(PQ\)の傾きは \(a≠0\) より
\(\displaystyle\frac{a^3-ta-(-8a^3+2ta)}{a-(-2a)}\)

\(=\displaystyle\frac{9a^3-3ta}{3a}\)

\(=3a^2-t\)

また点\(Q\)における接線の傾きは
\(y’=3(-2a)^2-t\)\(=12a^2-t\)

したがって直線\(PQ\)と点\(Q\)における接線が直交する条件は
\((3a^2-t)(12a^2-t)=-1\)・・・③

(3)

③において \(X=a^2\) とおくと

\((3X-t)(12X-t)=-1\)
整理して
\(36X^2-15tX+t^2+1=0\)・・・④

\(X\)の方程式④が正の解をただ1つもつとき、③を満たす正の数\(a\)がただ1つ存在する。

方程式④が正の解をただ１つもつときは次の場合が考えられる。
(i)正の重解をもつ
(ii)正の解を1つもち、0以下の解を1つもつ

ただし
\(f(X)=36X^2-15tX+t^2+1\)
とおくと、\(f(0)=t^2+1>0\) より、(ii)は不適であることが分かるので、(i)だけを考えればよい。

\(36X^2-15tX+t^2+1=0\) が重解をもつから \(D=0\) より

\((15t)^2-4\cdot36(t^2+1)=0\)
\(t^2=\displaystyle\frac{144}{81}\)
\(t=±\displaystyle\frac{4}{3}\)

ここで、重解は
\(X=\displaystyle\frac{15}{72}t\) だから
\(t=-\displaystyle\frac{4}{3}\) のときは、負の重解となり不適。

よって
\(t=\displaystyle\frac{4}{3}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線のなす角　back→二重接線