接線のなす角(直交)に関する例題です。
(例題)
2つの曲線
\(C_1:y=\cos x\)、\(C_2:y=\tan x\) (\(-\displaystyle\frac{π}{2}<x<\displaystyle\frac{π}{2}\)) がある。
(1)曲線\(C_1,C_2\)の交点を\(P\)とする。\(P\)における\(C_1\)の接線と\(C_2\)の接線のなす角\(θ\) (\(0≦θ≦π\)) を求めよ。
(2) (1)の交点\(P\)における2つの接線と\(x\)軸とで囲まれる三角形の面積を求めよ。
(解答)
(1)
(しかし、計算すると分かりますが分母が\(0\)になるので直交していることになります)
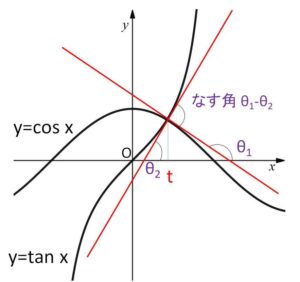
\(C_1:y=\cos x\)・・・①
\(C_2:y=\tan x\)・・・②
①と②の交点の\(x\)座標を\(t\)とおくと、(図より \(0<t<\displaystyle\frac{π}{2}\) となる)
\(\cos t=\tan t\)
つまり
\(\cos^2t=\sin t\)・・・③
③は\(\sin t\)に統一できるので、\(\sin t\) の値が具体的に求まります(\(t\)自体は分からない)。よって \(\cos t,\tan t\) も分かるので、必要になってくればこれらも使っていきます。
また①②を微分すると
\(y=-\sin x\)・・・①’
\(y=\displaystyle\frac{1}{\cos^2x}\)・・・②’
よって共有点における接線の傾きは
\(C_1\)では、\(-\sin t\)
\(C_2\)では、\(\displaystyle\frac{1}{\cos^2t}\)
\(\tan(θ_1-θ_2)=\displaystyle\frac{-\sin t-\displaystyle\frac{1}{\cos^2t}}{1+(-\sin t)\cdot(\displaystyle\frac{1}{\cos^2t})}\)
となりますが、③式から
(分母)\(=1-\sin t\cdot\displaystyle\frac{1}{\sin t}=0\)
となるので、直交することが分かります。解答にするなら、「接線の傾きの積=-1」を利用するとよいでしょう。
ここで接線の傾きの積は
\((-\sin t)\cdot(\displaystyle\frac{1}{\cos^2t})=(-\sin t)\cdot\displaystyle\frac{1}{\sin t}=-1\) (③より)
となるので、接線は直交する。
したがってなす角\(θ\)は、\(θ=\displaystyle\frac{π}{2}\)
(2)
③式より、具体的に\(\sin t\) (\(\cos t,\tan t\)) が分かるので、面積も具体的に求まります。
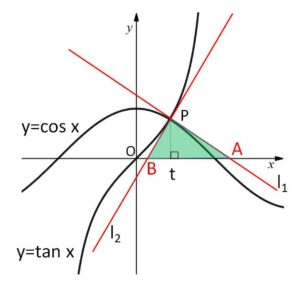
\(C_1:y=\cos x\)・・・①
\(C_2:y=\tan x\)・・・②
接線の方程式は
\(C_1\)での接線を\(l_1\)とすると
\(l_1:y=-\sin t(x-t)+\cos t\)・・・④
\(C_2\)では、接線を\(l_2\)とすると
\(l_2:y=\displaystyle\frac{1}{\cos ^2t}(x-t)+\tan t\)・・・⑤
\(l_1,l_2\)と\(x\)軸との交点をそれぞれ\(A,B\)とする。
\(A,B\)の\(x\)座標は、④⑤で\(y=0\)を代入することにより、それぞれ次のように求めることができる。
\(A:\ \displaystyle\frac{\cos t}{\sin t}+t\)
\(B:\ -\sin t\cos t+t\)
(底辺の長さ)=(\(A\)の\(x\)座標)-(\(B\)の\(x\)座標) です。
高さは、\(\cos t\), \(\tan t\) のどちらでもOKです。(最終的に③を使って整理すると同じ結果になる)
よって三角形の面積\(S\)は、
\(\cos^2t=\sin t\)・・・③ も用いると
\(S=\displaystyle\frac{1}{2}(\displaystyle\frac{\cos t}{\sin t}+\sin t\cos t)×\cos t\)
\(=\displaystyle\frac{1}{2}(1+\sin^2t)\)
ここで③より
\(1-\sin^2t=\sin t\)
\(\sin^2t+\sin t-1=0\)
\(0<t<\displaystyle\frac{π}{2}\) より、\(\sin t>0\) だから
\(\sin t=\displaystyle\frac{-1+\sqrt{5}}{2}\)
となるので、
\(S=\displaystyle\frac{1}{2}\left\{1+\displaystyle\frac{(-1+\sqrt{5})^2}{4}\right\}\)
\(=\displaystyle\frac{5-\sqrt{5}}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接する円と曲線 back→接する2曲線