接する円と曲線

接する円と曲線の例題です。

(例題)
\(xy\)平面において、直線 \(x=0\) を\(L\)とし、曲線 \(y=\log x\) を\(C\)とする。さらに、\(L\)上、または\(C\)上、または\(L\)と\(C\)との間にはさまれた部分にある点全体の集合を\(A\)とする。\(A\)に含まれ、直線\(L\)に接し、かつ曲線\(C\)と 点\((t,\log t)\) (\(0<t\)) において共通の接線をもつ円の中心を\(P_t\)とする。
\(P_t\)の\(x\)座標、\(y\)座標を\(t\)の関数として \(x=f(t)\)、\(y=g(t)\) と表したとき

(1)\(f(t)\) および \(g(t)\) を求めよ。
(2)\(\displaystyle\lim_{t \to 0}\displaystyle\frac{f(t)}{g(t)}\) を求めよ。

(解答)
(1)

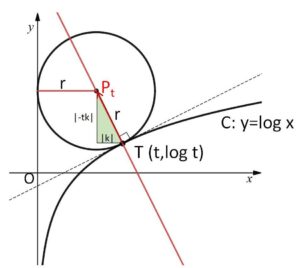
円の半径を\(r\ (>0)\)、円と曲線\(C\)の接点を \(T(t,\log t)\) とおく。

\(y=\log x\)　を微分すると
\(y’=\displaystyle\frac{1}{x}\)

円の中心は\(T\)における法線上にあるので、法線の傾きが\(-t\)であることから、実数\(k\)を用いると
\(\overrightarrow{TP_t}=k(1,-t)\)
となる。\(|\overrightarrow{TP_t}|=r\) だから
\(k^2(1+t^2)=r^2\)
\(k=±\displaystyle\frac{r}{\sqrt{1+t^2}}\)

図より(\(\overrightarrow{TP_t}\)は左上方向なので)、\(\overrightarrow{TP_t}\)の\(x\)成分は負の値になる。よって、\(k=-\displaystyle\frac{r}{\sqrt{1+t^2}}\)

ゆえに
\(\overrightarrow{OP_t}=\overrightarrow{OT}+\overrightarrow{TP_t}\)

\(=(t-\displaystyle\frac{r}{\sqrt{1+t^2}},\ \log t+\displaystyle\frac{rt}{\sqrt{1+t^2}})\)・・・①

(まず\(r\)を決定します)

また、円は \(x=0\) にも接するので、円の中心の\(x\)座標は\(r\)となるから
\(r=t-\displaystyle\frac{r}{\sqrt{1+t^2}}\)

\(r\)について解くと
\((1+\displaystyle\frac{1}{\sqrt{1+t^2}})r=t\)

\(r=\displaystyle\frac{t\sqrt{1+t^2}}{1+\sqrt{1+t^2}}\)

したがって
\(f(t)\)\(=r\)\(=\displaystyle\frac{t\sqrt{1+t^2}}{1+\sqrt{1+t^2}}\)

また①より
\(g(t)=\log t+\displaystyle\frac{t^2}{1+\sqrt{1+t^2}}\)

(2)
\(\displaystyle\lim_{t \to 0}\displaystyle\frac{f(t)}{g(t)}\)

\(=\displaystyle\lim_{t \to 0}\displaystyle\frac{t\sqrt{1+t^2}}{(1+\sqrt{1+t^2})\log t+t^2}\)

\(\left(\displaystyle\frac{0\sqrt{1}}{(1+\sqrt{1})(-\infty)+0}\right)\)

\(=0\)

以上になります。お疲れ様でした。
ここまで見ていただきありがとうございました。
next→ロルの定理と平均値の定理　back→共有点での接線のなす角