ロルの定理と平均値の定理

ロルの定理と平均値の定理について見ていきます。

・ロルの定理

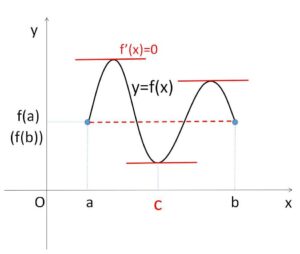
(解説)
簡単にまとめると、\(f(x)\)が定数関数のときは常に\(f'(x)=0\)となるので自明。定数関数でないときは、端点が \(f(a)=f(b)\) で等しいので、グラフに沿って動く点を考えると、\(x=a\)から出発して\(x=b\)に辿りつくまでにどこかで折り返す場所があり、そこの微分係数が\(0\)になるということです。

実数\(c\)が存在するということなので、数に関しては制限はなく、2個以上存在することもあります。

(証明)

(ア)\(f(x)\)が定数関数のとき
区間\((a,b)\)で、\(f'(x)=0\) なので、\(f'(c)=0\) となる\(c\)は無数に存在する。

(イ)\(f(x)\)が定数関数でないとき
\(f(x)\)が連続であるから、最大値・最小値の定理から区間\([a,b]\)で最大値および最小値をもつ。
また、定数関数でないことと \(f(a)=f(b)\) より、最大値または最小値の少なくとも一方は\(f(a)\ (f(b))\) ではない。そしてその値を\(f(c)\)とする。(\(a<c<b\))

(i)\(f(c)\)が最大値のとき
\(h\)を \(a<c+h<b\) を満たす絶対値が微小である数とする。

\(f(c)\) は最大値だから
\(f(c)-f(c+h)≧0\)・・・①　(\(f(c+h)\)も同時に最大値になる可能性もあるので=がつく)

\(h>0\) のとき
①の両辺を\(h\)で割って\(-1\)倍すると
\(\displaystyle\frac{f(c+h)-f(c)}{h}≦0\)・・・②

\(h<0\) のとき
同様に①より
\(\displaystyle\frac{f(c+h)-f(c)}{h}≧0\)・・・③

\(f(x)\)は \(x=c\) で微分可能だから、②③で \(h \to 0\) とすると
\(f'(c)≦0\)、 \(f'(c)≧0\)

ゆえに、\(f'(c)=0\)

(ii)\(f(c)\)が最小値のとき
(i)と同様に、\(f'(c)=0\) となることが示せる。

以上よりロルの定理が成り立つ。

※閉区間で連続、開区間で微分可能という条件について

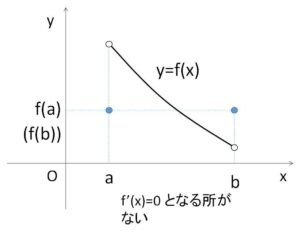
連続性を 開区間\((a,b)\) や \((a,b]\) などにすると、ロルの定理は成り立ちません(上図)。また証明の要となる最大値・最小値の定理も用いることができません。
微分可能性に関しては、閉区間にしても特に問題は無いですが、このロルの定理のほうが緩い条件になっています。

・平均値の定理①

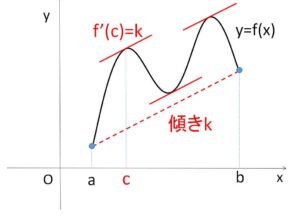
(解説)
ロルの定理を一般化したものが平均値の定理です。平均値の定理で \(f(a)=f(b)\) とすると、ロルの定理になります。
平均値の定理は、端点を通る直線の傾きと同じ値の微分係数が、区間内に存在するということを意味しています。これはグラフからも直感的に分かります。

また分母を払った
\(f(b)-f(a)=f'(c)(b-a)\)
の形もよく使われます。

証明については、\(f(x)\)と端点を通る直線の傾きをもつ直線・・・(※) との差をとった関数\(F(x)\)を考えて、端点での値が同じになるようにして、ロルの定理に帰着させます。(※については、今回の証明では端点を通る直線そのものを用いたいと思います。)

(証明)

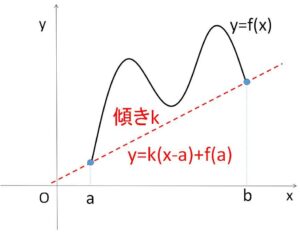
端点を通る直線の傾きを、\(k=\displaystyle\frac{f(b)-f(a)}{b-a}\) とおく。
この直線の方程式は
\(y=k(x-a)+f(a)\)

ここで
\(F(x)=f(x)-\{k(x-a)+f(a)\}\)・・・①
とおくと、\(F(x)\)も \([a,b]\)で連続で、\((a,b)\)で微分可能。

また
\(F(a)=f(a)-\{0+f(a)\}=0\)
\(F(b)=f(b)-\{f(b)-f(a)+f(a)\}=0\)
より、\(F(a)=F(b)\) となるので、ロルの定理より

\(F'(c)=0\)、\(a<c<b\)・・・②
となる\(c\)が存在する。

①より \(F'(x)=f'(x)-k\) だから
\(F'(c)=0\) は、\(f'(c)-k=0\)
つまり、\(f'(c)=k\) と同じことである。

したがってこれと②より
\(f'(c)=\displaystyle\frac{f(b)-f(a)}{b-a}\)、\(a<c<b\)
を満たす\(c\)が存在する。

・平均値の定理②
平均値の定理①は次のように表現されることもあります。

(解説)
「\(b\) → \(a+h\)」、「\(c\)の存在→\(θ\)の存在」になっていますが、内容は平均値の定理①のときと同じです。この平均値の定理の形式は、\(x=a\) (\(f(a)\)) を基準として関数の値がどれだけ変化するかに重きを置いています。(幅\(h\)とした微分の定義の式にも似ている)

(証明)
平均値の定理①より
\(\displaystyle\frac{f(a+h)-f(a)}{h}=f'(c)\)　 \((a<c<a+h)\)

分母を払って整理すると
\(f(a+h)=f(a)+hf'(c)\)　\((a<c<a+h)\)・・・①

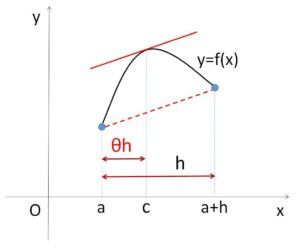
また図より、\(θ\)を \(0<θ<1\) を満たす定数とすると
\(c=a+θh\) と表すことができる。

よって①は
\(f(a+h)=f(a)+hf'(a+θh)\)　\((0<θ<1)\)
となり、この条件を満たす\(θ\)が存在することになる。

・平均値の定理を利用する場面
平均値の定理は利用するタイミングがやや難しい定理です。少しだけその利用する場面について話したいと思います。まずは、平均値の定理の意味(2端点の傾きと微分係数の関係)は大前提として抑えます。次に

\(\displaystyle\frac{f(b)-f(a)}{b-a}=f'(c)\)、\(a<c<b\)

は、2変数\(a,b\)に関する式を、1変数\(c\)の導関数に変換するものです。そして\(c\)が不等式によって挟まれているので、

・2変数の不等式の証明
・はさみうちを利用する極限

などに威力を発揮します。(もちろん\(f(x)\)の連続性や微分可能性が前提です)
代わりに導関数を考えればよいというところがポイントです。

また、平均値の定理は(\(c\)や\(θ\))の存在を明らかにする定理なので、存在に関する証明問題にもよく利用されます。

他には \(a_{n+1}=f(a_n)\) 型の数列の極限を求める際も平均値の定理を利用することが多いです。簡単に説明すると、極限値\(α\)が予想できるとき平均値の定理より

\(f(a_n)-f(α)=f'(c)(a_n-α)\)

となりますが、この形の漸化式の極限値は \(f(α)=α\) を満たすことがほとんどで

\(a_{n+1}-α=f'(c)(a_n-α)\)

と変形でき、両辺が1つずれた形になっているので、繰り返し漸化式を用いて(等比型なので)

\(a_n-α=\{f'(c)\}^{n-1}(a_1-α)\)

となり、あとは \(|f'(c)|<1\) が示せれば極限値が\(α\)となるという流れになります。

それと、\(f'(x)>0\) のとき関数の値が増加するという非常によく使う定理の証明にも平均値の定理が用いられます。
(\(f'(x)<0\)、\(f'(x)=0\) のときも同様です)

長くなったので演習は次回以降にします。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平均値の定理(c,θの具体例)　back→接する円と曲線