対数微分法と最大・最小値

対数微分法を利用する、最大最小値の問題です。

(例題)
関数 \(f(x)=x^x\) (\(x>0\)) と正の実数\(a\)について、以下の問いに答えよ。

(1)\(\displaystyle\frac{1}{4}≦x≦\displaystyle\frac{3}{4}\) における \(f(x)f(1-x)\) の最大値および最小値を求めよ。
(2)\(\displaystyle\frac{1}{4}≦x≦\displaystyle\frac{3}{4}\) における \(\displaystyle\frac{f(x)f(1-x)f(a)}{f(ax)f(a(1-x))}\) の最小値を求めよ。

(解答)
(1)

\(g(x)=f(x)f(1-x)\)・・・①  (\(\displaystyle\frac{1}{4}≦x≦\displaystyle\frac{3}{4}\))　とおく。

\(f(x)=x^x\) だから、\(g(x)>0\)。よって①で自然対数をとると
\(\log g(x)=\log f(x)+\log f(1-x)\)
\(\log g(x)=x\log x+(1-x)\log(1-x)\)

両辺\(x\)で微分して
\(\displaystyle\frac{g'(x)}{g(x)}=(\log x+1)+\{-\log(1-x)-1\}\)

\(=\log x-\log(1-x)\)

\(=\log\displaystyle\frac{x}{1-x}\)

\(=\log\displaystyle\frac{1}{\displaystyle\frac{1-x}{x}}\)

よって
\(g'(x)=g(x)\log\displaystyle\frac{1}{\displaystyle\frac{1}{x}-1}\)

\(g(x)>0\) だから、\(x=\displaystyle\frac{1}{2}\) を境目に\(g'(x)\)の符号が変わるので、増減表は次の通り。

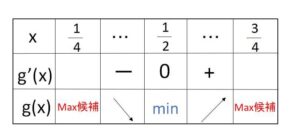
したがって
最大値については
\(g(\displaystyle\frac{1}{4})=f(\displaystyle\frac{1}{4})f(\displaystyle\frac{3}{4})\)
\(g(\displaystyle\frac{3}{4})=f(\displaystyle\frac{3}{4})f(\displaystyle\frac{1}{4})\)
より、両端で等しくなるので

最大値
\(g(\displaystyle\frac{1}{4})=(\displaystyle\frac{1}{4})^{\frac{1}{4}}\cdot(\displaystyle\frac{3}{4})^{\frac{3}{4}}\)
\(=\displaystyle\frac{\sqrt[4]{27}}{4}\)

最小値
\(g(\displaystyle\frac{1}{2})=(\displaystyle\frac{1}{2})^{\frac{1}{2}}\cdot(\displaystyle\frac{1}{2})^{\frac{1}{2}}\)
\(=\displaystyle\frac{1}{2}\)

(2)

\(h(x)=\displaystyle\frac{f(x)f(1-x)f(a)}{f(ax)f(a(1-x))}\)　(\(\displaystyle\frac{1}{4}≦x≦\displaystyle\frac{3}{4}\))　とおく。

ここで
\(\displaystyle\frac{f(a)}{f(ax)f(a(1-x))}\)

\(=\displaystyle\frac{a^a}{(ax)^{ax}\{a(1-x)\}^{a(1-x)}}\)

(\(a\)乗でまとめる)

\(=\left\{\displaystyle\frac{a}{(ax)^x\cdot\{a(1-x)\}^{(1-x)}}\right\}^a\)

\(=\left\{\displaystyle\frac{a}{a^x\cdot x^x\cdot a^{1-x}\cdot(1-x)^{1-x}}\right\}^a\)

\(=\left\{\displaystyle\frac{1}{x^x(1-x)^{1-x}}\right\}^a\)

\(=\{f(x)f(1-x)\}^{-a}\)

よって
\(h(x)=\{f(x)f(1-x)\}^{1-a}\)

したがって(1)より
\(\displaystyle\frac{1}{2}≦f(x)f(1-x)≦\displaystyle\frac{\sqrt[4]{27}}{4}\)
なので、\(h(x)\)の最小値は

\(0<a<1\) のとき
\((\displaystyle\frac{1}{2})^{1-a}\)

\(a=1\) のとき
\(1\)

\(a>1\) のとき
\((\displaystyle\frac{\sqrt[4]{27}}{4})^{1-a}\)

以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→第2次導関数と凹凸　back→最大・最小値と図形問題