極値と第2次導関数

第2次導関数を利用した極値の判定法について見ていきます。

・第2次導関数と極値
\(f(x)\)が微分可能であるとき、\(f'(a)=0\) を満たす \(x=a\) の前後で\(f'(x)\)の符号が入れかわるとき、\(f(a)\)は極値になります。

そこで\(f'(x)\)が連続のとき、極値をとる \(x=a\) 付近では、\(f'(x)\)は単調増加(減少)になることに着目すると、\(f(x)\)が2回微分可能(\(f(x),f'(x)\)の連続性が保証)で\(f”(x)\)が連続であるとき、次のことが成り立ちます。

(解説)

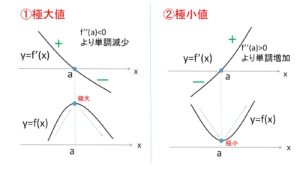
①について
\(f'(a)=0\)は必要条件。(これだけでは符号が変わるかどうか分からない)
これに、\(f”(a)<0\) の条件が加わることで、\(x=a\) 付近では\(f'(x)\)は単調減少関数になるから、\(f'(x)\)の正負は \(x=a\) を境目に「正→\(0\)→負」になる。
よって、\(f(a)\)は極大値となる。

②についても同様。

(例題)
関数 \(f(x)=\displaystyle\frac{x}{e^x}\)
の極値を第2次導関数を利用して求めよ。

(解答)
\(f'(x)=\displaystyle\frac{e^x-xe^x}{e^{2x}}=\displaystyle\frac{1-x}{e^{x}}\)

\(f”(x)=\displaystyle\frac{(-1)\cdot e^{x}-(1-x)\cdot e^{x}}{e^{2x}}\)

\(=\displaystyle\frac{x-2}{e^x}\)

\(f'(x)=0\) を満たすのは、\(x=1\)
また、\(f”(1)<0\) より
\(f(1)\) は極大値になる。

よって
極大値 \(f(1)=\displaystyle\frac{1}{e}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→グラフの概形まとめ(漸近線など)　back→第2次導関数と凹凸