グラフを書く例題です。
(例題)
\(f(x)=\displaystyle\frac{x^3+10x}{2(x^2+1)}\)
とするとき、増減、凹凸、漸近線を調べ、\(y=f(x)\) のグラフの概形を描け。
また、極値と変曲点を求めよ。
また対称性については、\(f(x)=\displaystyle\frac{x(x^2+10)}{2(x^2+1)}\)
より、\(x\)の部分が奇関数で、残りは偶関数なので、全体としては奇関数です。つまり原点対称になるので、\(x≧0\)の部分だけを考えればよいです。
(解答)
\(f(x)=\displaystyle\frac{x^3+10x}{2(x^2+1)}\)
\(f(-x)=\displaystyle\frac{-x^3-10x}{2(x^2+1)}=-f(x)\)
だから、\(y=f(x)\) のグラフは原点対称。
\(f(x)\)を微分すると
\(f'(x)=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{(3x^2+10)(x^2+1)-(x^3+10x)\cdot2x}{(x^2+1)^2}\)
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{x^4-7x^2+10}{(x^2+1)^2}\)・・・①
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{(x^2-5)(x^2-2)}{(x^2+1)^2}\)
また\(f'(x)\)を微分すると①より
\(f”(x)=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{(4x^3-14x)(x^2+1)^2-(x^4-7x^2+10)\{2(x^2+1)\cdot2x\}}{(x^2+1)^4}\)
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{(4x^3-14x)(x^2+1)-(x^4-7x^2+10)\cdot4x}{(x^2+1)^3}\)
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{18x^3-54x}{(x^2+1)^3}\)
\(=\displaystyle\frac{9x(x^2-3)}{(x^2+1)^3}\)
よって \(x≧0\) での増減表は次の通り。
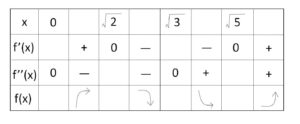
漸近線については
(\(x\)が有限のとき\(f(x)\)も有限なので、\(x\)軸に垂直な漸近線は無い)
\(\displaystyle\lim_{x \to ±\infty}\displaystyle\frac{f(x)}{x}\)
\(=\displaystyle\frac{x^2+10}{2(x^2+1)}\)
\(=\displaystyle\frac{1}{2}\)
\(\displaystyle\lim_{x \to ±\infty}\{f(x)-\displaystyle\frac{1}{2}x\}\)
\(=\displaystyle\frac{9x}{2(x^2+1)}\)
\(=0\)
よって漸近線の方程式は
\(y=\displaystyle\frac{1}{2}x\)
以上より、\(y=f(x)\) のグラフは次のようになる。
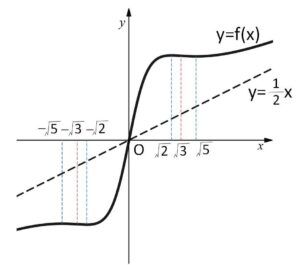
したがってグラフと増減表より
極大値
\(x=\sqrt{2},-\sqrt{5}\) のとき
\(f(\sqrt{2})=2\sqrt{2}\)
\(f(-\sqrt{5})=-\displaystyle\frac{5\sqrt{5}}{4}\)
極小値
\(x=\sqrt{5},-\sqrt{2}\) のとき
\(f(\sqrt{5})=\displaystyle\frac{5\sqrt{5}}{4}\)
\(f(-\sqrt{2})=-2\sqrt{2}\)
変曲点
\(x=0,±\sqrt{3}\) のとき
\((0,0)\)、\((\sqrt{3},\displaystyle\frac{13\sqrt{3}}{8})\)、\((-\sqrt{3},-\displaystyle\frac{13\sqrt{3}}{8})\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→グラフの増減と高次導関数 back→グラフの概形まとめ(漸近線など)